在这一篇笔记中我们来学习目前应用比较广泛的一个分类算法逻辑回归（Logistic Regression）。

什么是逻辑回归

首先大家应该有会有一个疑问，为什么既然叫逻辑回归，但是解决的却是分类问题呢。因为逻辑回归是将样本的特征和样本发生的概率联系起来，在拟合样本数据发生概率的时候，其实是在解决一个回归问题，当概率计算出来后，再根据概率进行分类处理。所以逻辑回归在解决分类问题时，其实中间还是进行了回归问题的处理，但是逻辑回归只能解决二分类问题，这一点要注意。

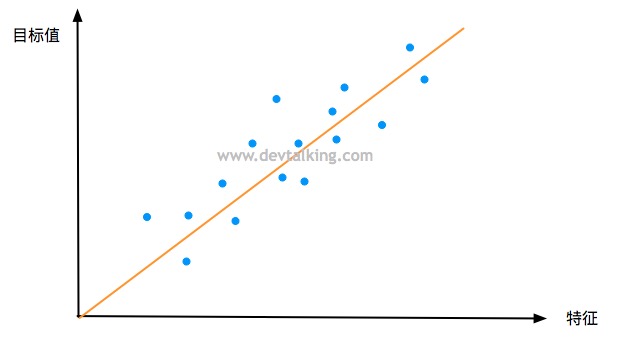
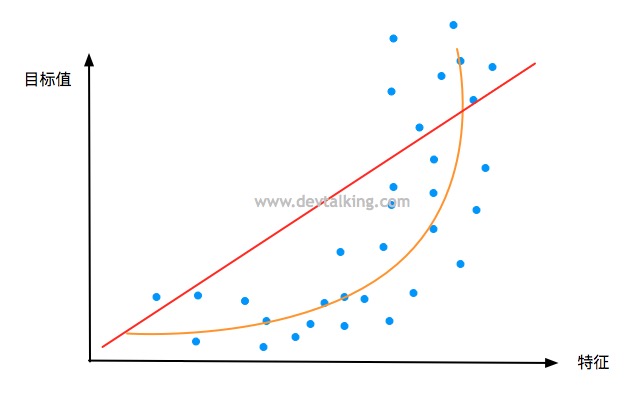
逻辑回归在解决概率这个回归问题时，和线性回归、多项式回归有一个不同的地方，那就是后者训练出的模型，预测其他样本数据的目标值时值域理论上是在负无穷到正无穷的，换句话说也就是对值域是没有什么限制的。而对于表示概率的数而言，一般值域都是在0到1之间，真实世界中，概率不都是按从0%到100%表示嘛。所以这就引出了逻辑回归和线性回归的相似和不同处，继而体现在公式模型上。在第四篇笔记中，我们知道多元线性回归的公式模型是：
$$ \hat y = \theta ^T X_b $$

因为$\hat y$的值域为$(-\infty,+\infty)$，所以如果要在逻辑回顾中运用在求解概率的公式模型上就需要另外一个函数将其值域限定在$(0, 1)$，我们将这个函数称为Sigmoid函数：

$$\hat p = \sigma(\theta ^T X_b)$$

$$\sigma(t) = \frac 1 {1+e^{-t}}$$

最终逻辑回归求解概率的模型为：

$$\hat p = \frac 1 {1+e^{-\theta ^T X_b}}$$

验证数据集与交叉验证

在上一篇笔记中我们又提到了训练数据集和测试数据集，拆分样本数据的这种做法目的就是通过测试数据集判断模型的好坏，如果我们发现训练出的模型产生了过拟合的现象，既在训练数据集上预测评分很好，但是在测试数据集上预测评分不好的情况，那可能就需要重新调整超参数训练模型，以此类推，最终找到一个或一组参数使得模型在测试数据集上的预测评分也很好，也就是训练出的模型泛化能力比较好。那么这种方式会产生一个问题，就是有可能会针对测试数据过拟合，因为每次都是找到参数训练模型，然后看看在测试数据集上的表现如何，这就让我们的模型又被测试数据集左右了，既可以理解为训练出的模型对特定的训练数据集和特定的测试数据集表现都不错，但是再来一种类似的样本数据，表现可能又不尽如人意了。

那么要彻底解决这个问题，就要引入验证数据集的概念，既将样本数据分为三份，训练数据集、验证数据集、测试数据集。

• 训练数据集和之前的用途一样，是用来训练模型的。
• 验证数据集的作用和之前的测试数据集一样，是用来验证由训练数据集训练出的模型的好坏程度的，或者说是调整超参数使用的数据集。
• 此时的测试数据集和之前的作用就不一样了，这里的测试数据集是当训练出的模型在训练数据集和验证数据集上都表现不错的前提下，最终衡量该模型性能的数据集。测试数据集在整个训练模型的过程中是不参与的。

交叉验证（Cross Validation）

我们在验证数据集概念的基础上，再来看看交叉验证。交叉验证其实解决的是随机选取验证数据集的问题，因为如果验证数据集是固定的，那么万一验证数据集过拟合了，那就没有可用的验证数据集了，所以交叉验证提供了随机的、可持续的、客观的模型验证方式。

交叉验证的思路是将训练数据分成若干份，假设分为A、B、C三份，分别将这三份各作为一次验证数据集，其他两份作为训练数据集训练模型，然后将训练出的三个模型评分取均值，将这个均值作为衡量算法训练模型的结果来调整参数，如果平均值不够好，那么再调整参数，再训练出三个模型，以此类推。

在前面的笔记中，我们使用的样本数据都是具有一定线性关系的，我们使用简单线性回归或者多元线性回归来拟合这些数据。但是这种具有强假设的数据集在实际应用中是比较少的，大多数的样本数据都没有明显的线性关系，那么这一节主要来看看如何对非线性关系的样本数据进行处理并预测。

多项式回归

多项式回归就是我们要使用的方法，其本质上还是基于线性回归的数学原理，只不过是对损失函数进行巧妙的改变使得原本我们用线性回归求得一条直线，变为求得一条曲线。

在线性回归的问题中，对于这些数据（蓝色点），我们是要寻找一条直线，让这条直线尽可能的拟合这些数据，如果数据只有一个特征的话，我们的模型就是：

$$ y=ax + b $$

$x$就是数据的已知特征，$a$和$b$是我们的模型需要求出的参数。

那如果我们的数据是像上图这种分布形态呢？显然红色那条直线无法拟合这些数据，而黄色那条曲线能更好的拟合这些数据。在样本数据特征数量不变的情况下，这条黄色曲线的模型其实就是一个一元二次方程：

$$y = ax^2+bx+c$$

我们抛开这个方程表示的坐标系形态来看，假设将$x^2$看作$x_1$，将$x$看作$x_2$，那么方式就可以写为：

$$y=ax_1+bx_2+c$$

这就变成了具有两个特征的样本数据的线性回归问题。现在大家就可以理解在本节开头所说的对损失函数进行巧妙改变的含义了吧。

所以对与多项式回归而言，就是需要我们为样本数据增加一个特征，使之可以用线性回归的原理更好的拟合样本数据，但是求出的是对于原始样本而言的非线性的曲线。

实现多项式回归

这一节我们在Jupyter Notebook中看看如何实现多项式回归：

import numpy as np
import matplotlib.pyplot as plt

# 构建样本数据，从-3到3的100个随机数
x = np.random.uniform(-3, 3, size=100)
# 转换为100行1列的矩阵，既样本数据只有一个特征
X = x.reshape(-1, 1)

# 求y的方程
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size=100)

# 将样本数据绘制出来
plt.scatter(x, y)
plt.show()

在机器学习的实际使用中，我们都希望有足够多的样本数据，并且有足够的特征来训练我们的模型，所以高维特征数据是经常会用到的，但是高维特征数据同样会带来一些问题：

• 机器学习算法收敛速度下降。
• 特征难于分辨，很难第一时间认识某个特征代表的意义。
• 会产生冗余特征，增加模型训练难度，比如说某一品牌型号汽车的特征数据，有从中国采集的，也有从国外采集的，那么就会产生公里/小时和英里/小时这种特征，但其实这两个特征代表的意义是一样的。
• 无法通过可视化对训练数据进行综合分析。

以上问题都是高维特征数据带来的普遍问题，所以将高维特征数据降为低维特征数据就很重要了。这篇笔记主要讲解机器学习中经常用到的降维算法PCA。

PCA是英文Principle Component Analysis的缩写，既主成分分析法。该算法能从冗余特征中提取主要成分，在不太损失模型质量的情况下，提升了模型训练速度。

理解PCA算法降维的原理

我们从二维降一维的场景来理解PCA降维的原理。上面的图示显示了一个二维的特征坐标，横坐标是特征1，纵座标是特征2。图中的五个点就表示了五条特征数据。我们先来想一下最简单粗暴的降维方式就是丢弃掉其中一个特征。

如上图中显示，将特征2抛弃，这里大家先注意一下这五个点落在特征1轴上的间距。

或者如上图所示抛弃特征1，大家再注意一下这五个点落在特征2轴上的间距。能很明显的发现，抛弃特征2，落在特征1轴上的五个点之间间距比较大，并且分布均匀。而抛弃特征1，落在特征2轴上的五个点之间间距大多都比较小，并且分布不均匀。

就这两种简单粗暴的降维方式而言，哪种更好一些呢？这里我们先来看看方差的概念，方差描述的是随机数据的离散程度，也就是离期望值（不严谨的说，期望值等同于均值）的距离。所以方差越大，数据的离散程度越高，约分散，离均值的距离越大。方差越小，数据的离散程度越小，约聚合，离均值的距离约小。那么大家可以想想作为机器学习算法训练的样本数据，每组特征应该尽可能的全，在该特征的合理范围内尽可能的广，这样才能更高的代表真实性，也就是每组特征数据的方差应该尽可能的大才好。所以就上面两种情况来看，抛弃特征2的降维方式更好一些。

这篇笔记主要介绍梯度下降法，梯度下降不是机器学习专属的算法，它是一种基于搜索的最优化方法，也就是通过不断的搜索然后找到损失函数的最小值。像上篇笔记中使用正规方程解实现多元线性回归，基于$X_b\theta$这个模型我们可以推导出$\theta$的数学解，但是很多模型是推导不出数学解的，所以就需要梯度下降法来搜索出最优解。

梯度下降法概念

我们来看看在二维坐标里的一个曲线方程：

纵坐标表示损失函数L的值，横坐标表示系数$\theta$。每一个$\theta$的值都会对应一个损失函数L的值，我们希望损失函数收敛，既找到一个$\theta$的值，使损失函数L的值最小。

在曲线上定义一点A，对应一个$\theta$值，一个损失函数L的值，要判断点A是否是损失函数L的最小值，既求该点的导数，在第一篇笔记中我解释过，点A的导数就是直线M的斜率，直线M是点A的切线，所以导数描述了一个函数在某一点附近的变化率，并且导数大于零时，函数在区间内单调递增，导数小于零时函数在区间内单调递减。所以$\frac {d L}{d \theta}$表示损失函数L增大的变化率，$-\frac {d L}{d \theta}$表示损失函数L减小的变化率。

再在曲线上定义一点B，在点A的下方，B点的$\theta$值就是A点的$\theta$值加上让损失函数L递减的变化率$-\eta \frac {d L}{d \theta}$，$\eta$称为步长，既B点在$-\frac {d L}{d \theta}$变化率的基础下移动了多少距离，在机器学习中$\eta$这个值也称为学习率。

同理还可以再求得点C，然后看是否是损失函数的L的最小值。所以梯度下降法就是基于损失函数在某一点的变化率$-\frac {d L}{d \theta}$，以及寻找下一个点的步长$\eta$，不停的找到下一个点，然后判断该点处的损失函数值是否为最小值的过程。$-\eta \frac {d L}{d \theta}$就称为梯度。

在第一篇笔记中将极值的时候提到过，当曲线或者曲面很复杂时，会有多个驻点，既局部极值，所以如果运行一次梯度下降法寻找损失函数极值的话很有可能找到的只是局部极小值点。所以在实际运用中我们需要多次运行算法，随机化初始点，然后进行比较找到真正的全局极小值点，所以初始点的位置是梯度下降法的一个超参数。

不过在线性回归的场景中，我们的损失函数$\sum_{i=1}^m(y^{(i)}-\hat y^{(i)})^2$是有唯一极小值的，所以暂时不需要多次执行算法搜寻全局极值。