在机器学习的实际使用中,我们都希望有足够多的样本数据,并且有足够的特征来训练我们的模型,所以高维特征数据是经常会用到的,但是高维特征数据同样会带来一些问题:
- 机器学习算法收敛速度下降。
- 特征难于分辨,很难第一时间认识某个特征代表的意义。
- 会产生冗余特征,增加模型训练难度,比如说某一品牌型号汽车的特征数据,有从中国采集的,也有从国外采集的,那么就会产生公里/小时和英里/小时这种特征,但其实这两个特征代表的意义是一样的。
- 无法通过可视化对训练数据进行综合分析。
以上问题都是高维特征数据带来的普遍问题,所以将高维特征数据降为低维特征数据就很重要了。这篇笔记主要讲解机器学习中经常用到的降维算法PCA。
PCA是英文Principle Component Analysis的缩写,既主成分分析法。该算法能从冗余特征中提取主要成分,在不太损失模型质量的情况下,提升了模型训练速度。
理解PCA算法降维的原理

我们从二维降一维的场景来理解PCA降维的原理。上面的图示显示了一个二维的特征坐标,横坐标是特征1,纵座标是特征2。图中的五个点就表示了五条特征数据。我们先来想一下最简单粗暴的降维方式就是丢弃掉其中一个特征。
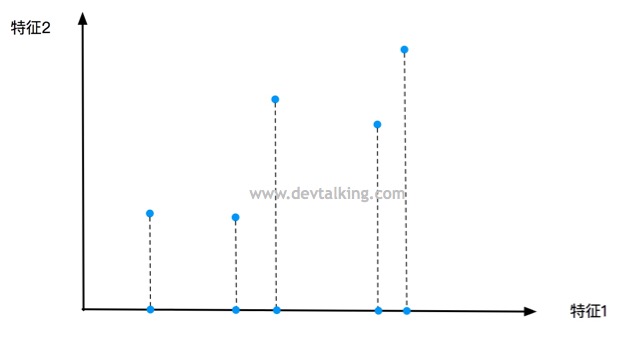
如上图中显示,将特征2抛弃,这里大家先注意一下这五个点落在特征1轴上的间距。

或者如上图所示抛弃特征1,大家再注意一下这五个点落在特征2轴上的间距。能很明显的发现,抛弃特征2,落在特征1轴上的五个点之间间距比较大,并且分布均匀。而抛弃特征1,落在特征2轴上的五个点之间间距大多都比较小,并且分布不均匀。
就这两种简单粗暴的降维方式而言,哪种更好一些呢?这里我们先来看看方差的概念,方差描述的是随机数据的离散程度,也就是离期望值(不严谨的说,期望值等同于均值)的距离。所以方差越大,数据的离散程度越高,约分散,离均值的距离越大。方差越小,数据的离散程度越小,约聚合,离均值的距离约小。那么大家可以想想作为机器学习算法训练的样本数据,每组特征应该尽可能的全,在该特征的合理范围内尽可能的广,这样才能更高的代表真实性,也就是每组特征数据的方差应该尽可能的大才好。所以就上面两种情况来看,抛弃特征2的降维方式更好一些。
但是简单粗暴的完全丢弃一个特征自然是不合理的,这极大的影响了训练出模型的正确性。所以,按照方差最大的理论,我们应该再找到一个特征向量,使样本数据落在这个特征向量后的方差最大,那么这个特征向量代表的特征就是我们需要的降维后的特征。这就是支撑PCA算法的理论之一。
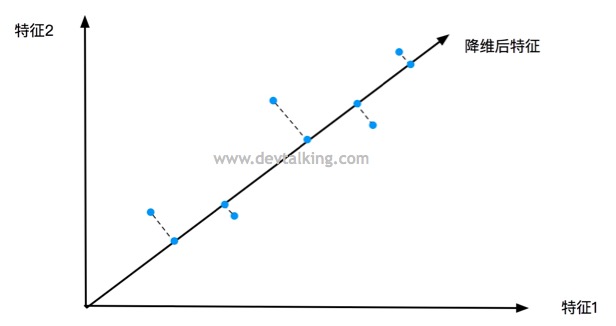
如上图所示,降维后的特征方差明显大于抛弃特征1或抛弃特征2后的方差。
我们在使用PCA之前首先需要对样本数据进行特征去均值化,也就是将每个特征的值减去该维特征的平均值。去均值化的目的是去除均值对数据变化的影响,也就是避免第一主成分收到均值的影响。
在第二篇笔记中,我们提到过方差,它的公式为:
$$ Var(X) = \frac{\sum_{i=1}^m(X_i-\overline X)^2} m $$
那么当数据去均值化后,公式中的$\overline X$就成了0,所以去均值后的方差为:
$$ Var(X) = \frac{\sum_{i=1}^mX_i^2} m $$
此时$X_i$就是降维后的特征,我们记为$X_p^{(i)}$,那么降维后特征值的方差公式为:
$$ Var(X_p) = \frac{\sum_{i=1}^m (X_p^{(i)})^2} m $$
因为在高维特征下,$X^{(i)}$和$X_p^{(i)}$都是向量,所以求方差时候应该对他们取模:
$$ Var(X_p) = \frac{\sum_{i=1}^m ||X_p^{(i)}||^2} m $$
所以我们就是要求上面这个公式的最大值。那么首先如何求得这个$X_p^{(i)}$
呢?我们来具体看一下:
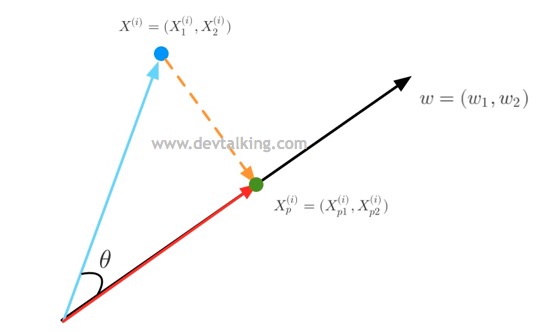
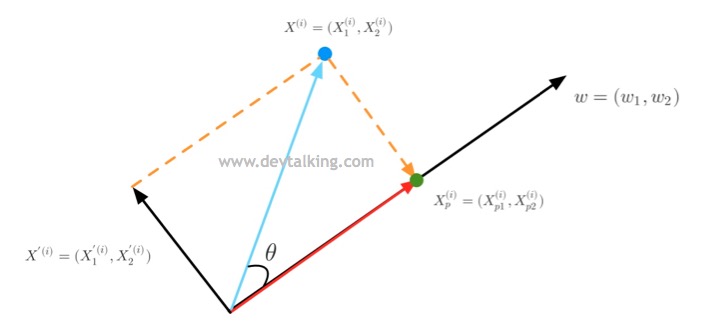
如上图所示,蓝色向量是特征值原始维度的向量,$w$黑色向量就是我们要寻求的新维度的向量,绿色的点就是蓝色点在新维度上的投影点,红色向量的长度就是投影点的特征值。下面我们先来看看初高中数学中学过的知识。
首先向量的点乘有代数定义,也有几何定义。在几何定义下,两个向量的点乘为这两个向量的长度相乘,再乘以这两个向量夹角的余弦:
$$ \vec{a} \cdot \vec{b} = |\vec{a}| \, |\vec{b}| \cos \theta $$
所以从上图来看:
$$X^{(i)} \cdot w=||X^{(i)}|| \cdot ||w|| \cdot \cos \theta$$
因为我们需要的$w$只是方向,所以它可以是一个方向向量,既长度为1,所以上面的公式就变为:
$$X^{(i)} \cdot w=||X^{(i)}||\cdot \cos \theta$$
然后由三角函数可知,夹角的余弦等于邻边除以斜边。上图中$\theta$角的斜边就是$||X^{(i)}||$,邻边就是$||X_p^{(i)}||$,所以:
$$||X_p^{(i)}||=||X^{(i)}|| \cdot \cos \theta$$
此时我们就知道了,我们要求得的红色向量的长度,既:
$$||X_p^{(i)}||=X^{(i)} \cdot w$$
代入上面的方差公式为:
$$ Var(X_p) = \frac{\sum_{i=1}^m ||X^{(i)} \cdot w||^2} m $$
因为两个向量的点乘是一个标量,所以最终公式为:
$$ Var(X_p) = \frac{\sum_{i=1}^m (X^{(i)} \cdot w)^2} m $$
那么我们的目标就是求$w$向量,使得上面的这个公式最大。上一篇笔记我们讲了用梯度下降法求函数极小值,那么这里我们就要用到梯度上升法求函数的极大值。
使用梯度上升法解决主成分分析问题
我们先将上面的公式展开(w是一个列向量):
$$ Var(X_p) = \frac{\sum_{i=1}^m (X^{(i)} \cdot w)^2} m\
=\frac 1 m \sum_{i=1}^m(X_1^{(i)}w_1+X_2^{(i)}w_2+…+X_n^{(i)}w_n)^2$$
既然是梯度上升,那么第一步当然是求梯度了,这和梯度下降是一样的,结合第五篇笔记中的梯度推导可得,上面公式的梯度为:
$$ \nabla f(w) = \begin{bmatrix}
\frac {\partial L}{\partial w_1} \\
\frac {\partial L}{\partial w_2} \\
… \\
\frac {\partial L}{\partial w_n} \\
\end{bmatrix} =\frac 2 m\begin{bmatrix}
\sum_{i=1}^m 2(X^{(i)}w)X_1^{(i)} \\
\sum_{i=1}^m 2(X^{(i)}w)X_2^{(i)} \\
… \\
\sum_{i=1}^m 2(X^{(i)}w)X_n^{(i)} \\
\end{bmatrix}$$
下面对上面的公式再进行向量化,这里我再推导一遍,首先我们将$X^{(i)}w$看成是一个1行m列的行矩阵中的元素:
$$\begin{bmatrix}X^{(1)}w& X^{(2)}w& X^{(3)}w& … &X^{(m)}w)\end{bmatrix}$$
然后将它和一个m行n列的矩阵相乘:
$$\begin{bmatrix}X^{(1)}w& X^{(2)}w& X^{(3)}w& … &X^{(m)}w)\end{bmatrix} \\
\cdot \begin{bmatrix}
X_1^{(1)}& X_2^{(1)}& X_3^{(1)}& … &X_n^{(1)} \\
X_1^{(2)}& X_2^{(2)}& X_3^{(2)}& … &X_n^{(2)} \\
X_1^{(3)}& X_2^{(3)}& X_3^{(3)}& … &X_n^{(3)} \\
… \\
X_1^{(m)}& X_2^{(m)}& X_3^{(m)}& … &X_n^{(m)} \\
\end{bmatrix}$$
因为X是一个m行n列矩阵,w是一个n行1列的矩阵,所以X乘w是一个m行1列的矩阵,上面我们将其转换为了1行m列的矩阵,所以上面的公式简写为$(Xw)^TX$,相乘后的结果是一个1行n列的矩阵:
$$(Xw)^TX=\begin{bmatrix}\sum_{i=1}^m(X^{(i)}w)X_1^{(i)}& \sum_{i=1}^m(X^{(i)}w)X_2^{(i)}& …& \sum_{i=1}^m(X^{(i)}w)X_n^{(i)} \end{bmatrix}$$
那我们的梯度是一个n行1列的矩阵,所以将上面的矩阵再做转置:
$$((Xw)^TX)^T=X^T(Xw)$$
所以最终主成分分析的梯度向量化后为:
$$\nabla f = \frac 2 m X^T(Xw)$$
代码实现PCA梯度上升
首先我们构建样本数据,其中有100条样本数据,每条样本数据中有2个特征:
import numpy as np |
接下来根据上文中讲到呃,下一步要对样本数据的每一个特征进行均值归0操作,也就是每一列的元素减去这一列所有元素的均值:
def demean(X): |
可以看到均值归0化后,样本数据的分布形态是没有变化的,但是坐标轴往右上移动了,既0点现在在样本数据的中间。下面来定义目标函数和梯度函数:
# 目标函数 |
在上面的公式推导的过程中提到过,我们期望的向量$w$是一个单位向量,所以在代码实现计算的时候需要将传入的初始向量$w$和计算后的新$w$向量都转换为单位向量(向量的单位向量为该向量除以该向量的模):
def direction(w): |
接下来的梯度上升计算和梯度下降计算基本是大同小异的:
# 参数传入样本矩阵,初始向量,步长,查找循环次数,两次方差的最小差值 |
在使用我们定义的方法前,有两点需要注意的是,一点是在PCA中,初始向量$w$不能为0,因为方差公式里$w$在分子,所以如果为0了,那么方差始终为0,所以每次我们随机初始化一个不为0的向量。另外一点是在PCA中我们不对样本数据做归一化或标准化处理,因为一旦做了归一化处理,样本数据的方差就变成了1,自然求不到最大方差了。
# 初始化随机向量 |

这样我们就求出了样本数据的第一个降维到的向量,我们称为样本的第一主成分。
求数据的其他主成分
在上节中我们使用的样本数据是在二维空间的,求出的第一主成分其实可以看作是将坐标轴旋转后横轴或纵轴,我们降维后的数据其实是新的坐标轴上某个轴的分量,那么另外一个分量自然是降维到垂直于第一主成分向量的向量,既新坐标轴的另外一个轴。该向量是第一主成分向量的正交线。那么下面我们来看一下第一主成分的正交线如何求:
从上图可以看到,$X^{‘(i)}$就是第一主成分向量$w$的正交线,由向量的加减法可得:
$$X^{‘(i)}=X^{(i)}-X_p^{(i)}$$
因为上文推导过:
$$X_p^{(i)}=||X_p^{(i)}|| w$$
$$||X_p^{(i)}||=X^{(i)} \cdot w$$
所以得:
$$X^{‘(i)}=X^{(i)}-(X^{(i)} \cdot w)w $$
这就相当于原始样本数据减去投影到第一主成分上的数据,我们对去掉第一主成分数据的样本数据再求第一主成分数据,那么就相当于在求原始样本数据的第二主成分了,以此类推就可以求得样本数据的n个主成分。
下面我们来用代码实现,首先我们算出样本数据在新坐标轴上的另一个分量,根据上面推导出的公式可得:
X2 = X - X.dot(w).reshape(-1, 1) * w |

首先可以看到,当样本数据去掉第一主成分数据后,另一个分量的数据其实就是在正交于第一主成分向量的轴上,所以所有点都在一条直线上。
然后将之前的gradient_ascent方法改个名称,因为它就是求第一主成分的方法,所以改名为first_component,然后求出X2的第一主成分:
def first_component(X, initial_w, eta, n_iters=1e4, different=1e-8): |
由向量的正交定理知道,垂直的向量点乘结果为0,所以我们来验证一下w和w2之间的点乘结果:
w.dot(w2) |
可以看到结果基于趋近于0。
下面我们封装一个计算n个主成分的方法:
def first_n_component(n, X, eta=0.01, n_iters=1e4, different=1e-8): |
高维数据向低维数据映射
我们再来回顾一下PCA降维的基本原理,首先要做的事情就是对样本数据寻找另外一个坐标系,这个坐标系中的每一个轴依次可以表达样本数据的重要程度,既主成分。我们取出前k个主成分,然后就可以将所有的样本数据映射到这k个轴上,既获得了一个低维的数据信息。
$$X=\begin{bmatrix}
X_1^{(1)}& X_2^{(1)}& … &X_n^{(1)} \\
X_1^{(2)}& X_2^{(2)}& … &X_n^{(2)} \\
… \\
X_1^{(m)}& X_2^{(m)}& … &X_n^{(m)}
\end{bmatrix}$$
上面的$X$是样本数据,该样本数据有m行,n个特征,既是一个n维的样本数据。
$$W_k=\begin{bmatrix}
W_1^{(1)}& W_2^{(1)}& … &W_n^{(1)} \\
W_1^{(2)}& W_2^{(2)}& … &W_n^{(2)} \\
… \\
W_1^{(k)}& W_2^{(k)}& … &W_n^{(k)} \\
\end{bmatrix}$$
假设上面的$W$是样本数据$X$的主成分向量矩阵,每一行代表一个主成分向量,一共有k个主成分向量,每个主成分向量上有n个值。
我们已经推导出了求映射后的向量的大小,也就是每一行样本数据映射到该主成分上的大小为:
$$||X_p^{(i)}||=X^{(i)} w$$
那如果将一行有n个特征的样本数据分别映射到k个主成分上,既得到有k个值的新向量,既降维后的,有k个特征的新样本数据。所以我们需要的就是$X$矩阵的第一行和$W$矩阵的每一行对应元素相乘然后再相加,$X$矩阵的第二行和$W$矩阵的每一行对应元素相乘然后再相加,以此类推就可以求出降维后的,m行k列的新矩阵数据:
$$X^{‘}=XW_k^T$$
$X^{‘}$就是降维后的数据,既然可以降维,那么我们也可从数学的角度将降维后的数据还原回去。$X^{‘}$是m行k列的矩阵,$W_k$是k行n列的矩阵,所以$X^{‘} W_k$就是还原后的m行n列的原矩阵。那为什么说是从数学角度来说呢,因为毕竟已经从高维降到了低维,那势必会有丢失的数据信息,所以还原回去的数据也不可能和原始数据一样的。
在PyCharm中封装PCA
我们在myML中新建一个类PCA:
import numpy as np |
在Jupyter Notebook中使用封装的PCA
首先构建样本数据:
import numpy as np |
然后导入我们封装好的PCA类,训练主成分并根据主成分对样本数据降维:
# 导入我们封装的PCA类 |
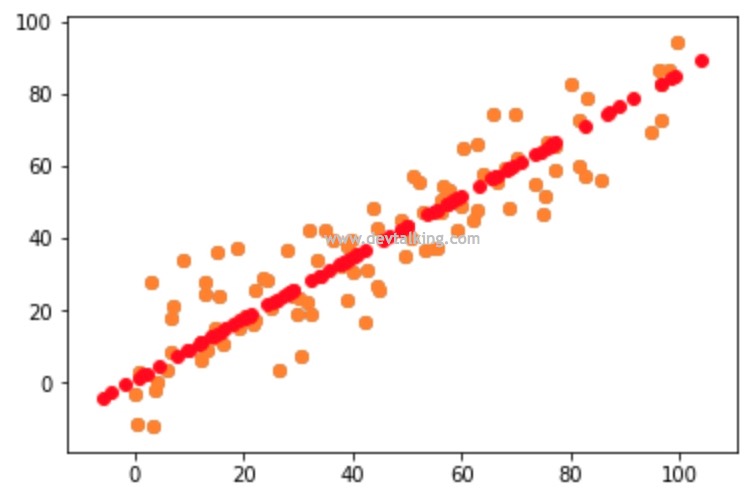
看到我们非常简单地就把一个二维特征的样本数据根据主成分映射为了一维特征的样本数据。同时我们还可以将其恢复二维特征数据:
# 恢复样本数据维度 |

在前面提到过,从高维降到低维就已经有部分信息丢失了,所以再恢复回去后势必不会和原始数据一样。从上图中可以看到,恢复后的二维特征数据其实是在一条直线上,而这条直线其实就是原始样本数据的主成分。
Scikit Learn中的PCA
这一节我们来看看Scikit Learn中封装的PCA如何使用,
import numpy as np |
可以看到,我们封装PCA类时,使用标准的机器学习算法的模式,所以在使用Scikit Learn提供的PCA时,几乎是一样的。
使用真实的数据
这一节我们使用真实的数据来体会一下PCA的威力。我们使用Scikit Learn中提供的手写数字数据:
import numpy as np |
可以看到,Scikit Learn提供的手写数据是一个64维特征的样本数据,一共有1797行,也就是一个1797行,64列的矩阵。
我们先用KNN分类算法来计算这个样本数据:
# 首先将样本数据拆分为训练数据集和测试数据集 |
从上面的代码可以看出,使用KNN算法对样本数据进行训练时通过网格搜索的邻近点为5个,使用了明可夫斯基距离,但是p是2,所以其实还是欧拉距离,并且没有使用距离权重。训练后的分类准确率为98.7%,在我的电脑上耗时38.1毫秒。
下面我们先简单粗暴的将这个64维特征的样本数据降至2维特征数据,然后再用KNN算法训练一下看看情况:
# 使用Scikit Learn提供的PCA |
从上面的代码和结果可以看到,首先使用KNN算法训练的耗时从64维时的38.1毫秒降至了1.77毫秒,所以这验证了PCA降维的其中的减少计算时间的作用。但是当我们查看分类准确率的时候发现非常低,所以说明我们降维度的降的太低,丢失了太多的数据信息。那么PCA中的超参数n_components应该如何取呢?其实Scikit Learn的PCA提供了一个方法就是可以计算出每个主成分代表的方差比率:
pca.explained_variance_ratio_ |
比如通过explained_variance_ratio_我们可以知道通过PCA分析出的手写数据的前两个主成分的方差比率为14.6%和13.7%,加起来既标识降维后的数据只能保留了原始样本数据38.3%的数据信息,所以自然分类准确率很差了。那么如果我们使用PCA将64维数据计算出64个主成分,然后看看每个主成分的方差比率是如何变化的:
pca = PCA(n_components=X_train.shape[1]) |
可以看到上面64个方差比率是从大到小排序的,而且后面的方差率越来越小,所以从这个数据我们其实已经可以计算出一个合适的主成分个数,使其方差比率之和达到一个极大值。我们将维数和方差率绘制出来看看:
# 横轴为维数,纵轴为每个维度对应的之前所有维度的方差率之和 |
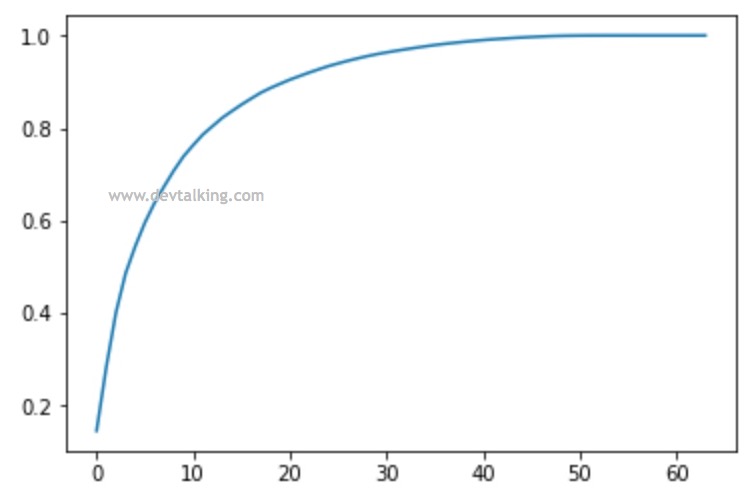
从图中可以看到,当维度数在30左右的时候,方差率上升已经很平缓了,所以从这个图中都可以目测出,我们将64维特征的样本数据降维至30维左右是比较合适的。
其实Scikit Learn的PCA提供了一个参数,就是我们期望达到的总方差率为多少,然后会帮我们自动计算出主成分个数:
# 传入一个0到1的小数,既总方差率 |
可以看到,我们期望的总方差率为95%时的主成分数为28。然后我们再使用KNN来训练一下降为28维特征的样本数据,看看准确率和时间为多少:
# 对原始训练数据和原始测试数据进行降维 |
从上面代码的结果可以看到,在使用KNN训练28维特征的数据时耗时也只有2.44毫秒,但是分类准确率达到了98%。比64维特征的数据耗时减少了15倍,但是准确率只减少了0.6%。这个性价比是非常之高的,这就是PCA的威力所在。
使用PCA对数据进行降噪
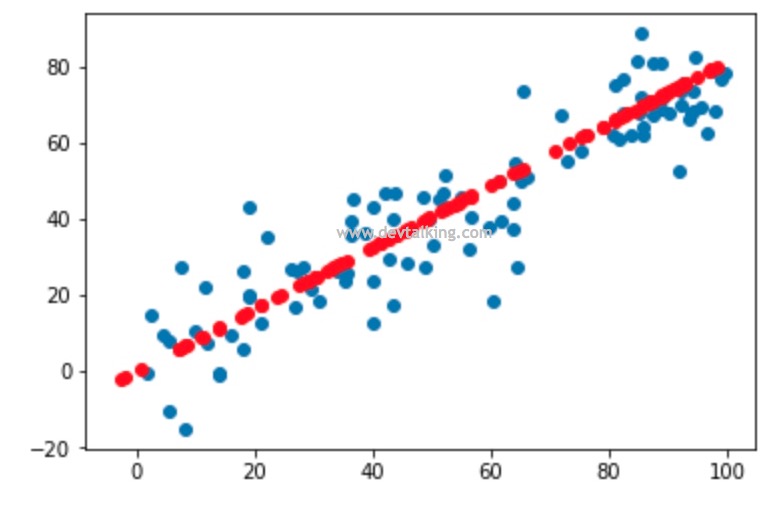
这张图是之前小节中生成的,其中蓝色的点是我们构建的原始样本数据,红色的点是经过PCA降维后,又通过PCA还原维度的样本数据。对这个图我们可以这样理解,原始样本数据的分布都在这条红色点组成的直线上下,而导致这些蓝色点没有落在红色直线上的原因就是因为数据有噪音,所以通过PCA降维其实是去除了数据的噪音。但这些噪音也是也是数据信息,所以通常我们说使用PCA对数据进行降维后会丢失一些数据信息。
下面我们通过一个实际的例子来看一下PCA的降噪过程。我们依然使用手写识别的例子,我们手写识别的样本数据中加一些噪音,然后看PCA如何去除这些噪音:
import numpy as np |

从图中可以看出,手写数字的识别度非常差。下面我们使用PCA对example_digits进行降噪处理:
from sklearn.decomposition import PCA |
当我们只保留50%主成分的时候,特征维度从64维降到了12维。然后我们再将其还原为64维,既过滤掉了噪音:
example_components_inverse = pca.inverse_transform(example_components) |

可以看到,此时图片中的手写数字的识别度有明显的提升。这就是PCA降噪的作用。
人脸识别
PCA有一个典型的实际应用,就是人脸识别。我们这一节就来简单看看PCA在人脸识别中的应用。
首先我们还是先从PCA的原理来说,PCA就将高维数据降至相对的低维数据,但是这些低维的数据却能反应了原始高维数据的绝大多数主要特征。那么由PCA训练出的这些主成分其实就代表了原始数据的主要特征。那么如果原始高维数据是一张张不同的人脸数据时,那么由PCA训练出的主成分其实就是这一张张人脸的主要特征,称为特征脸。好比,爷爷,爸爸,儿子三个人长的很像,其实是这三张人脸有共同的特征脸。下面我们就使用Scikit Learn中提供的人脸数据来看看特征脸的应用。
import numpy as np |
如果网络不好的朋友,可以去这里手动下载All images aligned with funneling数据集,然后在使用fetch_lfw_people()时需要增加data_home这个参数,指定你存放数据集的目录,比如fetch_lfw_people(data_home='/XXX/XXX')然后执行,Scikit Learn就会去你指定的目录下解压lfw_funneled压缩包,抓取数据。从上面代码结果可以看到,这个人脸的数据集一共有13233张人脸图片,每张人脸图片有2914个特征,其实也就是由2914个不同值的像素组成,通过faces.images.shape我们知道这13233张图片的大小是62乘以47像素,相乘的值正好就是2914。
因为这个数据集里人脸的分布并不均匀,所以我们在用之前先将其进行随机处理:
# 求一个随机索引 |

然后我们通过PCA求出这个13233条样本数据,2914维特征数据集的所有主成分。所有主成分要等于小于样本数据的特征数量。下面来求这个样本数据集的最大维度:
from sklearn.decomposition import PCA |

从代码结果可以看出,主成分的方差比率由大到小排序,第一个主成分能表示23.33%的人脸特征,从图上也能看到,第一个图显示了一个人脸的整个脸庞,第二个图显示了人脸的五官位置等。图中的这些脸就是特征脸,可以清晰的看到特征脸依次显示人脸特征的变化过程。
申明:本文为慕课网liuyubobobo老师《Python3入门机器学习 经典算法与应用》课程的学习笔记,未经允许不得转载。