这一节继续优化甜甜圈主体部分，从下面这张真实的照片可以看出，甜甜圈主体表面是坑坑洼洼的（任何面点食物应该都不会很光滑），而目前我们的甜甜圈主体太过光滑，所以显得有点假。

给甜甜圈增加质感

首先点击Edit菜单，选择Preferences，打开Blender设置菜单，然后选择Add-ons，在右侧搜索框搜索node，然后将Node: Node Wrangle插件打上勾。这个插件可以优化和加速节点效果的处理流程。

这一节我们来优化甜甜圈的主体部分，目前我们只是捏出了形状和简单的设置了基本颜色，看上去还是有点假。所以我们通过使用Texture Paint能力将其完善的更加真实一些。

先来看一张真实的甜甜圈照片，可以看到在主体部分的腰部凹陷那一圈，颜色是比较浅的，因为那个部位被烘烤的力度较小，越是顶部和底部，颜色会越深，这和我们煎炸其他食品的道理是一样的。

Texture Paint

在使用Texture Paint之前，我们先看看材质、纹理等这些概念的区别和关系。

这一节来继续完善甜甜圈上的糖粒，我们需要完成两件事：

1. 给糖粒上色，而且是随机上色。
2. 给糖衣铺上其他形状、形态的糖粒。

给糖粒随机上色

通过上一节实操，我们知道甜甜圈糖衣上的糖粒是通过对糖衣添加了粒子效果实现的，而粒子的对象是一个母板糖粒，所以我们要更改糖粒的颜色，只能针对这个模板糖粒进行修改。

我们可以修改糖粒的颜色，但是可以看到糖衣上的所有糖粒都是同一种颜色。

这一节继续对糖衣进行完善，先来看一张实图：

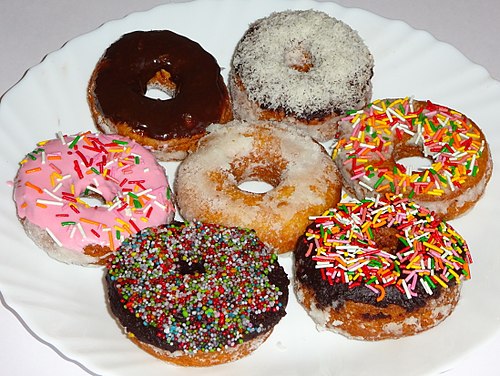
可以看到糖衣上有五颜六色的糖粒（我猜应该是糖），呈小圆柱体，不规则的铺在糖衣上面。这一节就来实现糖衣上的小糖粒。

整理对象

首先我们先通过集合的方式，对目前场景里的对象做一下分类和整理。选中一个或若干个对象，按下M，然后选择New Collection，就可以将对象放在一个集合中，在《用Blender做甜甜圈学习笔记五 - 雕刻糖衣白模》中使用过。

为甜甜圈和糖衣创建Donut集合，将充当桌面的平面放在Environment集合中，将摄像机和灯光放在Cam & Light集合中。

到目前位置，甜甜圈的模型基本都调整、雕刻完毕了，接下来需要将我们做的模型渲染出来看看效果。在渲染之前，我们需要先认识一个对于渲染很重要的元素，灯光。

在整个视图中，除了甜甜圈的对象以外，我们应该也早已发现了另外两个对象，Light和Camera。

灯光

灯光的强弱可以通过灯光离物体的距离以及一些设置项来调整，比如我们将灯光移动到离甜甜圈比近的位置，然后选择右上角的渲染模式视图，可以看到甜甜圈被强光照的都发白了。