在这一篇笔记中我们来学习目前应用比较广泛的一个分类算法逻辑回归(Logistic Regression)。
什么是逻辑回归
首先大家应该有会有一个疑问,为什么既然叫逻辑回归,但是解决的却是分类问题呢。因为逻辑回归是将样本的特征和样本发生的概率联系起来,在拟合样本数据发生概率的时候,其实是在解决一个回归问题,当概率计算出来后,再根据概率进行分类处理。所以逻辑回归在解决分类问题时,其实中间还是进行了回归问题的处理,但是逻辑回归只能解决二分类问题,这一点要注意。
逻辑回归在解决概率这个回归问题时,和线性回归、多项式回归有一个不同的地方,那就是后者训练出的模型,预测其他样本数据的目标值时值域理论上是在负无穷到正无穷的,换句话说也就是对值域是没有什么限制的。而对于表示概率的数而言,一般值域都是在0到1之间,真实世界中,概率不都是按从0%到100%表示嘛。所以这就引出了逻辑回归和线性回归的相似和不同处,继而体现在公式模型上。在第四篇笔记中,我们知道多元线性回归的公式模型是:
$$ \hat y = \theta ^T X_b $$
因为$\hat y$的值域为$(-\infty,+\infty)$,所以如果要在逻辑回顾中运用在求解概率的公式模型上就需要另外一个函数将其值域限定在$(0, 1)$,我们将这个函数称为Sigmoid函数:
$$\hat p = \sigma(\theta ^T X_b)$$
$$\sigma(t) = \frac 1 {1+e^{-t}}$$
最终逻辑回归求解概率的模型为:
$$\hat p = \frac 1 {1+e^{-\theta ^T X_b}}$$
Sigmoid函数
我们先来看看这个Sigmoid函数为什么将值域限定在$(0, 1)$,将这个函数绘制出来看一下:import numpy as np
import matplotlib.pyplot as plt
# 定义Sigmoid函数
def sigmoid(t):
return 1 / (1 + np.exp(-t))
# 构建向量x,随机生成500个数,范围从-10到10
x = np.linspace(-10, 10, 500)
# y值通过Sigmoid计算出
y = sigmoid(x)
plt.plot(x, y)
plt.show()
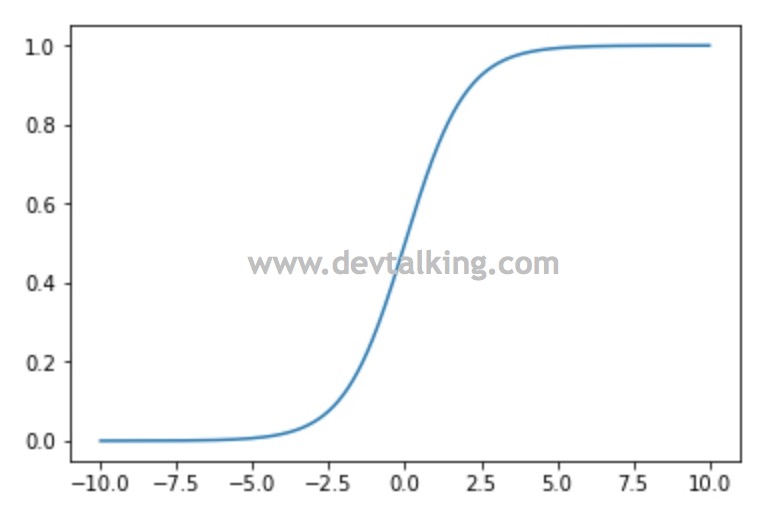
从曲线图可以看出,$y$的值最小不会小于0,最大不会大于1,表明了它的值域是$(0, 1)$,我将Sigmoid函数再写出来看一下:
$$\sigma(t) = \frac 1 {1+e^{-t}}$$
当$t$无穷大时,$e^{-t}$无穷小,那么当1除以无穷小时,它的值就无限接近于1。那么当$t$无穷小时,$e^{-t}$无穷大,那么当1除以无穷大时,它的值就无限接近于0。
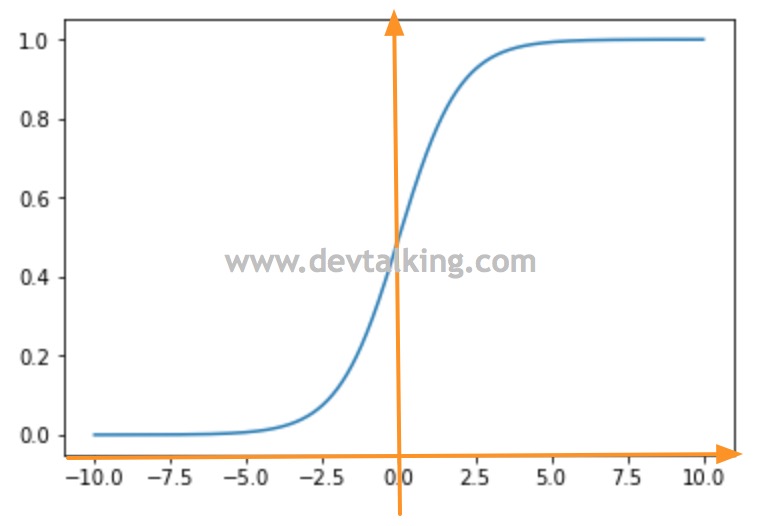
我将坐标轴在Sigmoid曲线图上绘制出来,可以看到当$t > 0$时,越接近0,概率$p$越接近0.5,$t$越远离0时,概率$p$越大于0.5,并且当$t$大到一定程度时,概率$p$基本稳定在1附近。当$t < 0$时,越接近0,概率$p$越接近0.5。$t$越远离0时,概率$p$越小于0.5,并且当$t$小到一定程度时,概率$p$基本稳定在0附近。这就是Sigmoid函数在逻辑回归中的数学意义。
逻辑回归的损失函数
我们再将逻辑回归中计算概率的公式写出来:
$$\hat p = \frac 1 {1+e^{-\theta ^T X_b}}$$
现在的问题是我们如何求出上面的$\theta$值,也就是在逻辑回归问题中,损失函数如何定义。
前面说过,逻辑回归只能解决二分类问题,既当概率估计值$\hat p$大于等于0.5时,我们记$\hat y$为1,当$\hat p$小于等于0.5时,记$\hat y$为0,既:
$$\hat y =\left\{
\begin{aligned}
1, \ \ \ \hat p \ge 0.5 \\
0, \ \ \ \hat p \leq 0.5 \\
\end{aligned}
\right.
$$
那么我们先将损失函数也分为两种情况来看:
$$cost = \left\{
\begin{aligned}
如果y=1,p越小,cost越大(损失越大) \\
如果y=0,p越大,cost越大(损失越大)\\
\end{aligned}
\right.
$$
也就是说,在真实的分类为1的情况下,如果概率越小,那么说明损失越大,因为概率越小,分类应该越趋向0。在真实的分类为0的情况下,如果概率越大,那么也说明损失越大,因为概率越大,分类应该越趋向1。
上面我们只是根据逻辑回归分类的方式,定义出了逻辑回归损失函数的损失趋势和语言解释,那么我们需要在数学的海洋中找到符合这种趋势的数学工具,或者说函数。再次之前,我们先来回顾一下高中学过的数学知识对数。
对数
在数学中,如果有$x=\alpha ^y$,$y$是$\alpha$的指数,那么可以说以$\alpha$为底$x$的对数是$y$,记为:
$$y=log_{\alpha}x$$
对数有一些简便的写法:
- 如果底数为2,可以省略底数记为$log \ x$
- 如果底数为10,可以省略底数记为$lg \ x$
- 如果底数为$e$,可以省略底数记为$ln \ x$
对数的主要作用是解幂比如:
- $log_{\theta} \ xy = log_{\theta} \ x + log_{\theta} \ y$
- $log_{\theta} \ \frac x y = log_{\theta} \ x - log_{\theta} \ y$
- $log_{\theta} \ x^y = y log_{\theta} \ x$
- $log_{\theta} \ \sqrt[y]{x} = \frac {log_{\theta} \ x} y$
对数的存在使得求这种复杂幂的问题更快更方便。
我们再来看看对数在几何意义上的曲线: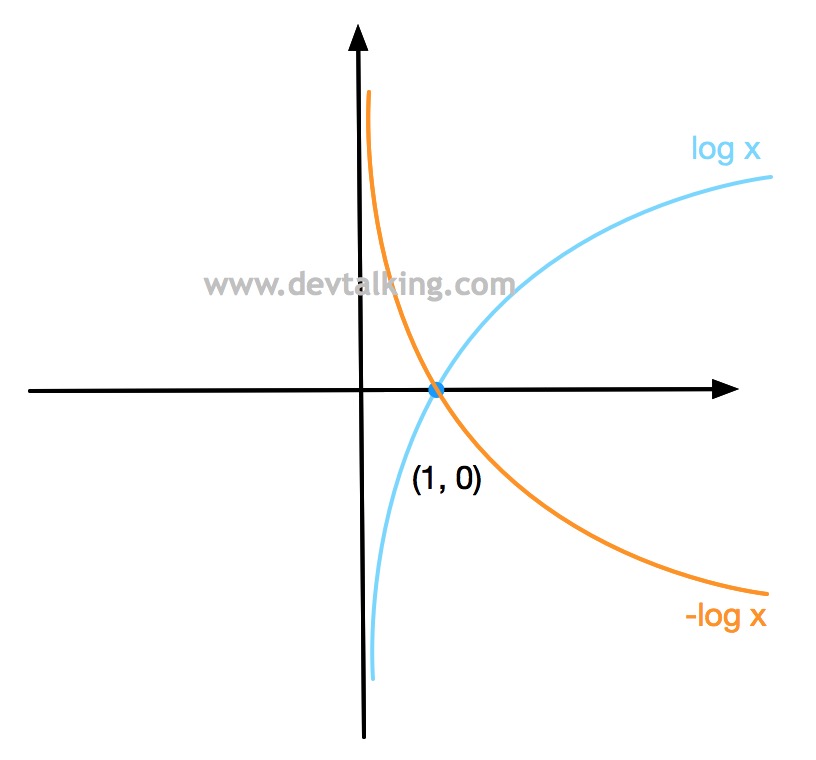
可以很容易的算出,对数的曲线始终是过$(1, 0)$点的。
定义损失函数
回顾完对数后,我们再来看看逻辑回归的损失函数,没错,我们就是要使用对数的函数来表示:
$$cost = \left\{
\begin{aligned}
{如果y=1,那么损失函数为:-log(\hat p) \\
如果y=0,那么损失函数为:-log(1-\hat p)}
\end{aligned}
\right.
$$
我们来看看这两个函数为什么符合之前我们定义的损失函数的描述。首先$-log x$的曲线为:
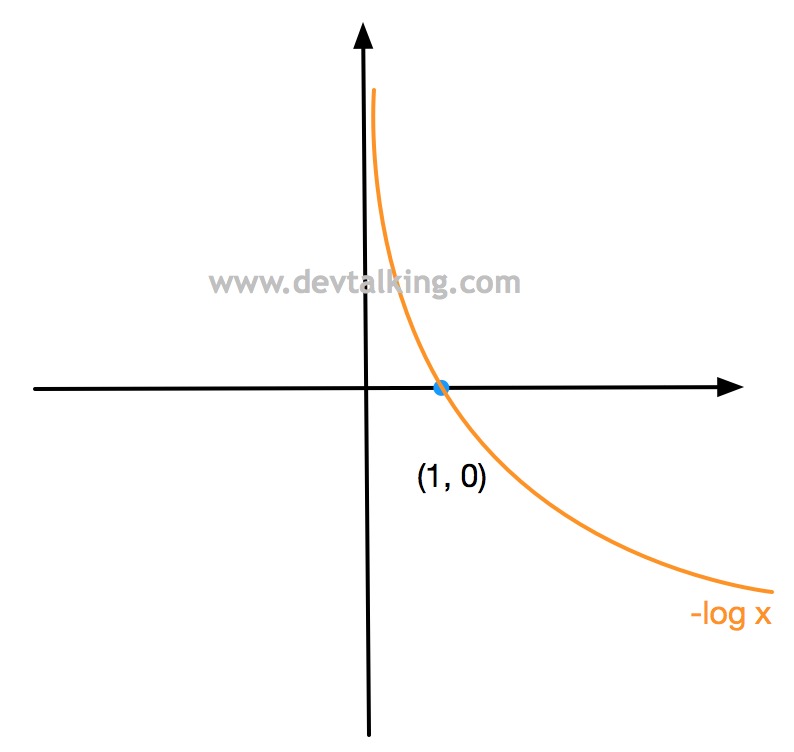
之前说了,概率的值域在$(0,1)$之间,所以上图曲线的x轴以下的曲线是没有意义的,所以对于$-log (\hat p)$,它的曲线是:

从上面的曲线图可以很容易的发现,当$\hat p$趋近于0的时候,$-log (\hat p)$趋近于正无穷,这个正无穷其实就是一个很大的损失惩罚,因为当$\hat p$趋近于0时,$y$应该也是趋近于0,但是这里$y$定义的是1。当$\hat p$在不断趋近1的过程中,$-log (\hat p)$的值逐渐减小,既损失逐渐减小,当$\hat p$趋近于1时,$y$应该也是趋近于0,和这里定义的是一致的,所以$-log (\hat p)$的值是0,说明没有损失。
下面再来看看$-log(1-x)$的曲线:
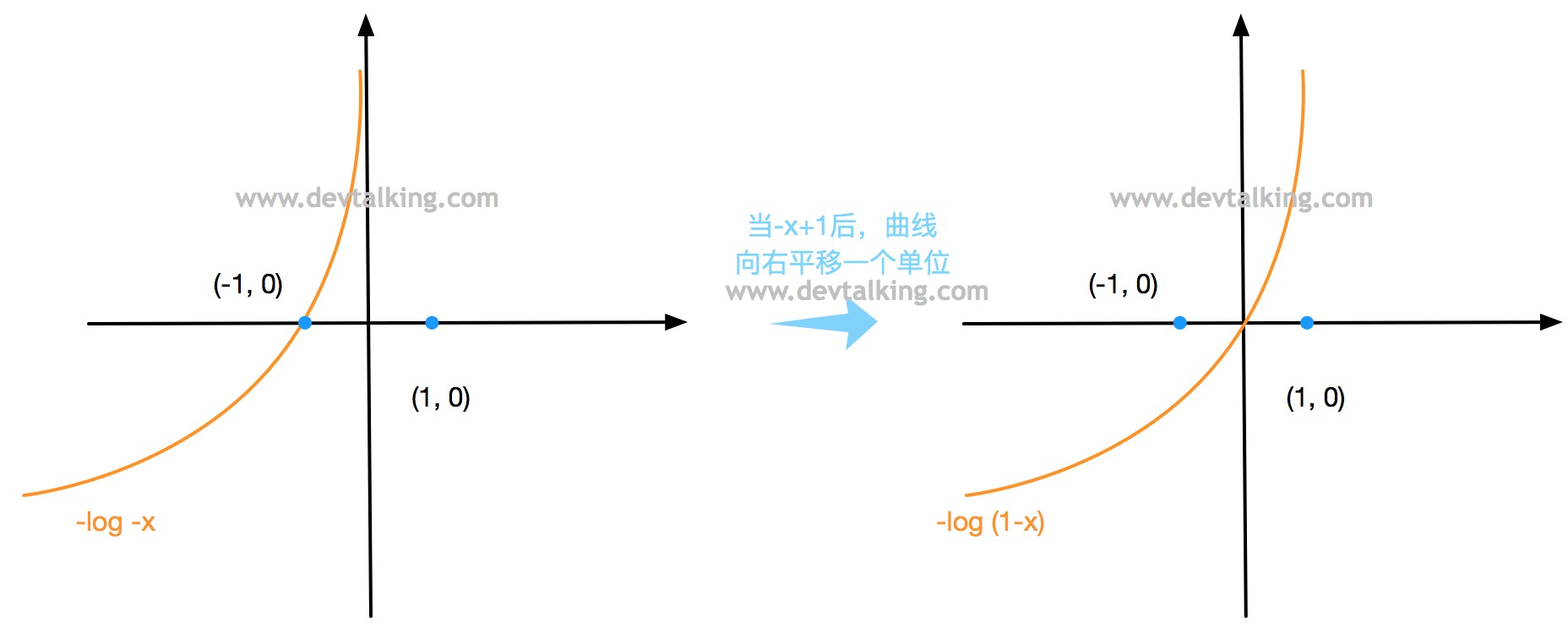
同理因为概率的值域在$(0, 1)$之间,所以$-log(1-\hat p)$的曲线为:
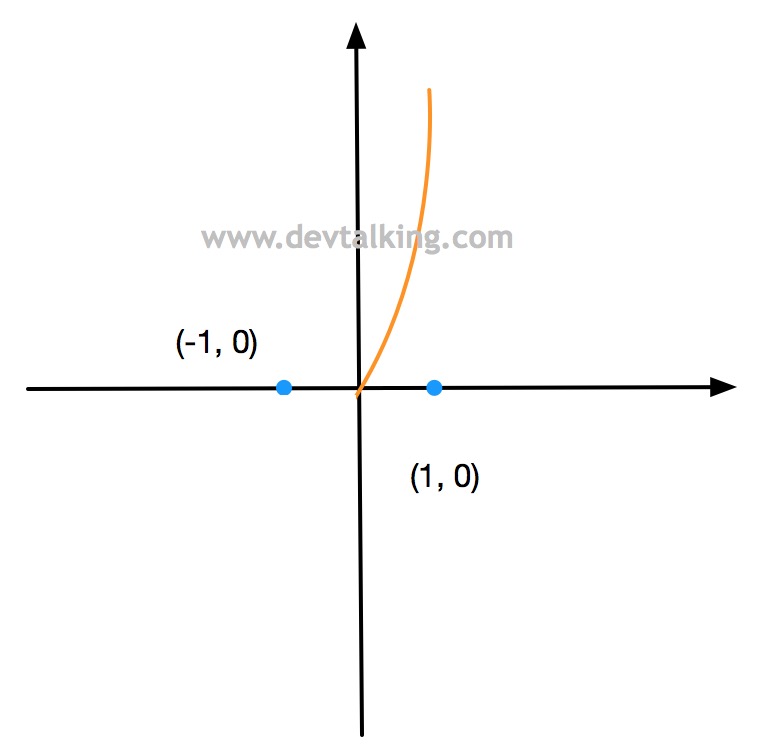
这条曲线同样可以解释我们之前定义的损失趋势。
此时我们找到的损失函数还是根据不同的分类分成了两个,其实将其合成一个也很简单:
$$cost=-ylog(\hat p)-(1-y)log(1-\hat p)$$
如此一来,当$y=0$时,损失函数为$-log(1-\hat p)$,当$y=1$时,损失函数为$-log(\hat p)$。
上面的公式,是针对一个样本数据的,那么如果有多个样本数据,其实就是将这些样本数据的损失值加起来然后在求一下平均值:
$$\hat p = \frac 1 {1+e^{-\theta ^T X_b}}$$
$$L(\theta)=-\frac 1 m \sum_{i=1}^my^{(i)}log(\hat p^{(i)})+(1-y^{(i)})log(1-\hat p^{(i)})$$
下面我们要做的就是找到一组$\theta$值,使得上面的$L(\theta)$达到最小值。
损失函数的梯度
上面的公式是没法像线性回归那样求出一个正规方程解的,所以我们需要使用梯度下降法来求得使$L(\theta)$最小的一组$\theta$。下面我们先把公式都列出来:
- 多元线性回归公式:$ \hat y = X_b \theta $,注意这里的$X_b$是加上了值全部为1的一列的矩阵,而为了方便推导,这里的$\theta$是一个列向量,就不写成$\theta^T$了。
- Sigmoid函数:$\sigma(t) = \frac 1 {1+e^{-t}} $。
- 逻辑回归概率公式:$\hat p = \sigma(X_b \theta) =\frac 1 {1+e^{-X_b \theta}} $
- 逻辑回归损失函数:$L(\theta)=-\frac 1 m \sum_{i=1}^m(y^{(i)}log(\sigma(X_b^{(i)} \theta))+(1-y^{(i)})log(1-\sigma(X_b^{(i)} \theta))) $
在第五篇笔记中我们知道,求损失函数的梯度就是对$\theta$这个列向量逐个元素求导:
$$\nabla L(\theta)=\begin{bmatrix}
\frac {\partial L(\theta)} {\partial \theta_0} \\
\frac {\partial L(\theta)} {\partial \theta_1} \\
\frac {\partial L(\theta)} {\partial \theta_2} \\
… \\
\frac {\partial L(\theta)} {\partial \theta_n} \\
\end{bmatrix}$$
我们从里往外来看,先从Sigmoid函数求导入手。
Sigmoid函数求导
先变换一下Sigmoid函数:
$$\sigma(t)=\frac 1 {1+e^{-t}} = (1 + e^{-t})^{-1}$$
然后对Sigmoid函数求导,这里遵循求导链式法则以及求导基本法则:
- 复合函数 $(f\circ g)(x)$的导数$(f\circ g)’(x)$为:$(f\circ g)’(x)=f’(g(x))g’(x)$
- 代数函数导数:$\frac {dx^n} {dx} = nx^{n-1} \ \ \ (x \neq 0)$
- 数学常数的指数求导还是它自己:$\frac {de^x} {dx}=e^x$
所以可得Sigmoid函数的导数为:
$$\sigma(t)^{‘} = (-1)(1+e^{-t})^{-2} \cdot e^{-t} \cdot (-1) =
(1+e^{-t})^{-2} \cdot e^{-t}
$$
Sigmoid函数的对数求导
下面再往外扩展,来看一下$log(\sigma(t))$的导数。这里遵循的导数法则为:
- 对以2为底的对数求导:$\frac {dlogx} {dx} = \frac 1 x$
- 复合函数 $(f\circ g)(x)$的导数$(f\circ g)’(x)$为:$(f\circ g)’(x)=f’(g(x))g’(x)$
所以$log(\sigma(t))$的导数为:
$$log(\sigma(t))^{‘} = \frac 1 {\sigma(t)} \cdot \sigma(t)^{‘}=\\
\frac 1 {(1+e^t)^{-1}} \cdot (1+e^{-t})^{-2} \cdot e^{-t} = \\
(1+e^{-t})^{-1} \cdot e^{-t}=\frac {e^{-t}} {1+e^{-t}}=\\
\frac {1+e^{-t}-1} {1+e^{-t}} = 1-\frac 1 {1+e^{-t}}=\\
1-\sigma(t)
$$
$log(1-\sigma(t))$的导数为:
$$log(1-\sigma(t))^{‘}=\frac 1 {1-\sigma(t)} \cdot (-\sigma(t))^{‘}=\\
\frac 1 {1- \frac 1 {1+e^{-t}}} \cdot (1+e^{-t})^{-2} \cdot e^{-t} \cdot -1=\\
\frac {(1+e^{-t})^{-1}} {e^{-t}} \cdot e^{-t} \cdot -1 = \\
-(1+e^{-t})^{-1} = -\sigma(t)
$$
逻辑回归损失函数求导
当我们知道了Sigmoid函数和Sigmoid函数的对数的求导结果后,我们对逻辑回归损失函数求导就很容易了(这里对第$j$个$\theta$求导),先来看前半部分:
$$\frac {d(y^{(i)}log(\sigma(X_b^{(i)} \theta)))} {d\theta_j}=\\
y^{(i)} \cdot (1-\sigma(X_b^{(i)} \theta)) \cdot X_j^{(i)}
$$
最后的那个$X_j^{(i)}$是第$j$个$\theta$前面的系数,再来看后半部分:
$$\frac {d((1-y^{i})log(1-\sigma(X_b^{(i)} \theta)))} {d\theta_j}=\\
(1-y^{(i)}) \cdot (-\sigma(X_b^{(i)} \theta)) \cdot X_j^{(i)}
$$
此时对整个损失函数求导就是上面两部分相加:
$$\frac {d(L(\theta))} {d(\theta_j)}=-\frac 1 m \sum_{i=1}^m (y^{(i)} \cdot (1-\sigma(X_b^{(i)} \theta)) \cdot X_j^{(i)} + (1-y^{(i)}) \cdot (-\sigma(X_b^{(i)} \theta)) \cdot X_j^{(i)})= \\
-\frac 1 m \sum_{i=1}^m(y^{(i)}X_j^{(i)}-y^{(i)}\sigma(X_b^{(i)} \theta) \cdot X_j^{(i)}-\sigma(X_b^{(i)} \theta) \cdot X_j^{(i)} + y^{(i)}\sigma(X_b^{(i)} \theta) \cdot X_j^{(i)})= \\
-\frac 1 m \sum_{i=1}^m(y^{(i)}X_j^{(i)}-\sigma(X_b^{(i)} \theta) \cdot X_j^{(i)})= \\
-\frac 1 m \sum_{i=1}^m(y^{(i)}-\sigma(X_b^{(i)} \theta)) \cdot X_j^{(i)})= \\
\frac 1 m \sum_{i=1}^m(\sigma(X_b^{(i)} \theta)-y^{(i)})X_j^{(i)}
$$
所以逻辑回归损失函数的梯度为:
$$\nabla L(\theta)=\frac 1 m \begin{bmatrix}
\sum_{i=1}^m(\sigma(X_b^{(i)} \theta)-y^{(i)}) \\
\sum_{i=1}^m(\sigma(X_b^{(i)} \theta)-y^{(i)})X_1^{(i)} \\
\sum_{i=1}^m(\sigma(X_b^{(i)} \theta)-y^{(i)})X_2^{(i)} \\
… \\
\sum_{i=1}^m(\sigma(X_b^{(i)} \theta)-y^{(i)})X_n^{(i)} \\
\end{bmatrix}$$
大家再来回顾一下第五篇笔记中线性回归的梯度:
$$\nabla L(\theta) = \frac 2 m\begin{bmatrix}
\sum_{i=1}^m (X_b^{(i)}\theta-y^{(i)})\\
\sum_{i=1}^m (X_b^{(i)}\theta-y^{(i)})X_1^{(i)} \\
\sum_{i=1}^m (X_b^{(i)}\theta-y^{(i)})X_2^{(i)} \\
…\\
\sum_{i=1}^m (X_b^{(i)}\theta-y^{(i)})X_n^{(i)} \\
\end{bmatrix}$$
可以发现这两个梯度在形态上是非常相似的,因为线性回归的梯度通过向量化可以优化为:
$$\nabla L(\theta) =\frac 2 m X_b^\top(X_b \theta - y)$$
所以逻辑回归的梯度最终可以写为:
$$\nabla L(\theta) =\frac 1 m X_b^\top(\sigma(X_b \theta) - y)$$
实现逻辑回归算法
因为逻辑回归拟合损失函数使用的是梯度下降法,所以我们封装逻辑回归算法时大部分都可以套用我们之前封装的线性回归梯度下降方法,需要修改的只是损失函数、预测和评分里的一些代码。
import numpy as np |
下面我们在Jupyter Notebook中使用Scikit Learn提供的鸢尾花数据验证我们封装的逻辑回归的方法:
import numpy as np |
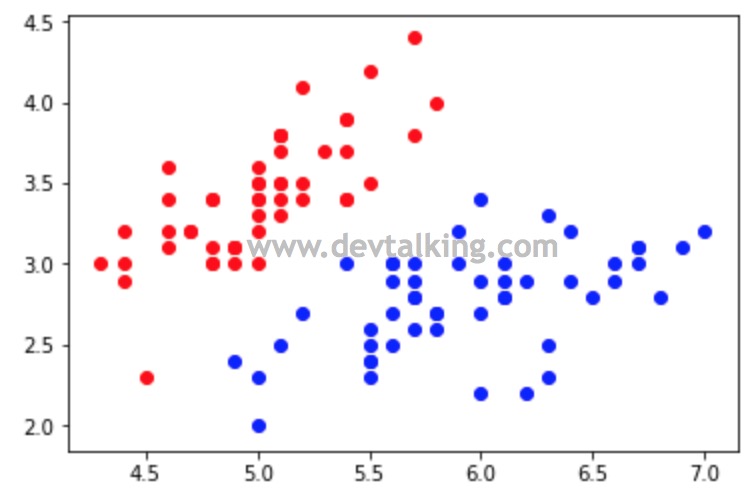
因为鸢尾花数据中有三类鸢尾花,而逻辑回归在一开始就讲过是一个解决二分类问题的算法,所以我们只取前两类的鸢尾花数据来验证,并且只用每类鸢尾花的前两个特征,方便绘图:
# 只取前两类的鸢尾花数据 |
from myML.LogisticRegression import LogisticRegression |
可以看到我们封装的逻辑回归算法对鸢尾花的分类是100%准确的,当然也是因为当前的数据比较简单。
申明:本文为慕课网liuyubobobo老师《Python3入门机器学习 经典算法与应用》课程的学习笔记,未经允许不得转载。