机器学习笔记八之多项式回归、拟合程度、模型泛化

在前面的笔记中，我们使用的样本数据都是具有一定线性关系的，我们使用简单线性回归或者多元线性回归来拟合这些数据。但是这种具有强假设的数据集在实际应用中是比较少的，大多数的样本数据都没有明显的线性关系，那么这一节主要来看看如何对非线性关系的样本数据进行处理并预测。

多项式回归

多项式回归就是我们要使用的方法，其本质上还是基于线性回归的数学原理，只不过是对损失函数进行巧妙的改变使得原本我们用线性回归求得一条直线，变为求得一条曲线。

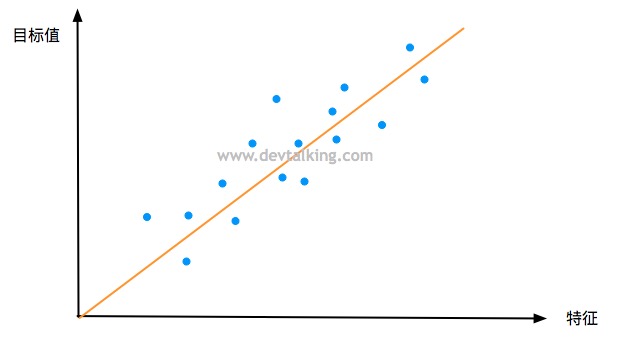
在线性回归的问题中，对于这些数据（蓝色点），我们是要寻找一条直线，让这条直线尽可能的拟合这些数据，如果数据只有一个特征的话，我们的模型就是：

$$ y=ax + b $$

$x$就是数据的已知特征，$a$和$b$是我们的模型需要求出的参数。

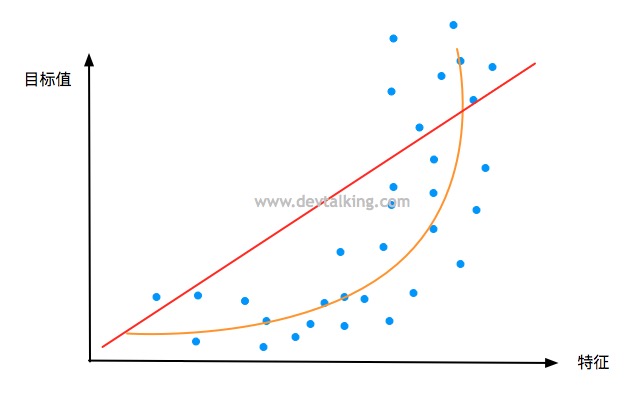
那如果我们的数据是像上图这种分布形态呢？显然红色那条直线无法拟合这些数据，而黄色那条曲线能更好的拟合这些数据。在样本数据特征数量不变的情况下，这条黄色曲线的模型其实就是一个一元二次方程：

$$y = ax^2+bx+c$$

我们抛开这个方程表示的坐标系形态来看，假设将$x^2$看作$x_1$，将$x$看作$x_2$，那么方式就可以写为：

$$y=ax_1+bx_2+c$$

这就变成了具有两个特征的样本数据的线性回归问题。现在大家就可以理解在本节开头所说的对损失函数进行巧妙改变的含义了吧。

所以对与多项式回归而言，就是需要我们为样本数据增加一个特征，使之可以用线性回归的原理更好的拟合样本数据，但是求出的是对于原始样本而言的非线性的曲线。

实现多项式回归

这一节我们在Jupyter Notebook中看看如何实现多项式回归：

import numpy as np
import matplotlib.pyplot as plt

# 构建样本数据，从-3到3的100个随机数
x = np.random.uniform(-3, 3, size=100)
# 转换为100行1列的矩阵，既样本数据只有一个特征
X = x.reshape(-1, 1)

# 求y的方程
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size=100)

# 将样本数据绘制出来
plt.scatter(x, y)
plt.show()

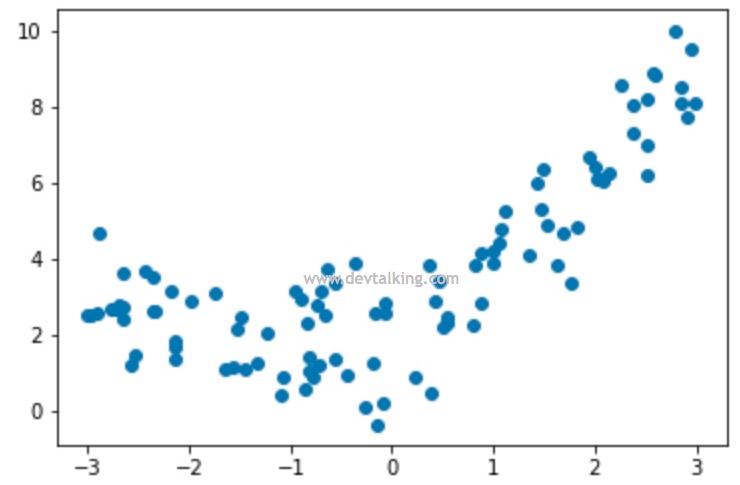
可以看到，我们的样本数据很明显是非线性的分布形态。下面我们先用线性回归直接来拟合这些样本数据看看：

# 导入线性回归类
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
# 训练模型
lr.fit(X, y)
# 预测出y值
y_predict = lr.predict(X)

# 绘制拟合直线
plt.scatter(x, y)
plt.plot(x, y_predict, color='r')
plt.show()

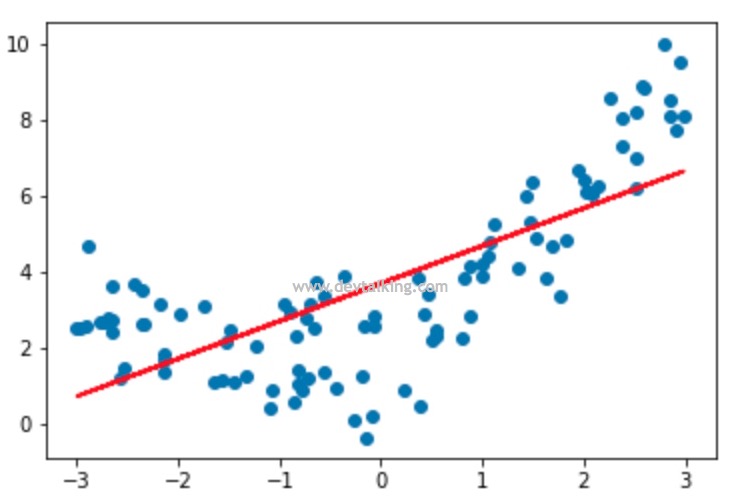
可以看到这条直线明显无法很好的拟合这些样本数据。下面我们来看看如何使用多项式回归来拟合样本数据：

# 根据上文中讲的，我们需要先给样本数据增加一个特征，既X的平方
X2 = X**2
# 通过np.hstack方法将原始特征和平方后的特征转换为新的特征矩阵，既100行2列的特征矩阵
X_new = np.hstack((X, X2))

X_new.shape
# 结果
(100, 2)

# 然后再对新的样本特征用线性回归训练模型
lr2 = LinearRegression()
lr2.fit(X_new, y)
y_predict_new = lr2.predict(X_new)

# 绘制出拟合曲线
plt.scatter(x, y)
plt.plot(np.sort(x), y_predict_new[np.argsort(x)], color='r')
plt.show()

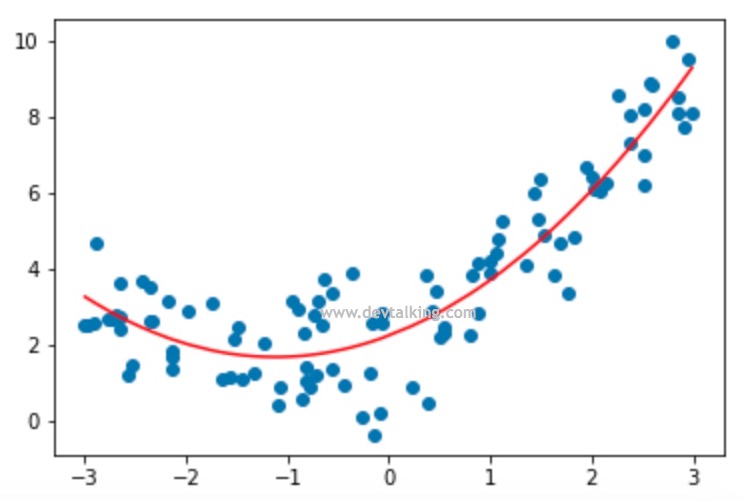
这里在绘制拟合曲线时有点技巧，我们使用np.sort(x)对样本数据x数组从小到大排序，也就是从x数组中最小的元素开始绘制，然后使用np.argsort(x)求出数组x从小到大元素的索引，然后通过y_predict_new[np.argsort(x)]就可以求得数组x从小到大元素对应的y值了。否则拟合曲线绘制出来是不连续的，大家可以试一下只传入x和y_predict_new，看看绘制出的曲线是什么样的。

我们再来看看训练出的系数和截距：

lr2.coef_
# 结果
array([ 1.01051072,  0.45036129])

lr2.intercept_
# 结果
2.2249327738612221

可以看到，第一个特征的系数是1，第二个特征的系数，既对第一个特征做了平方的系数是0.45，截距是2.2。这和我们在之前构建的求y的方程是非常近似的，因为求y的方程里还加了正态分布的噪音，所以系数和截距是有点误差的，但是误差不大。那这就是多项式回归的原理和实现思路。我们在讲PCA的时候知道它的作用主要是给样本数据降维，而多项式回归是给样本数据升维，所以不同的算法，不同的样本数据是有降维，也有升维的，这点需要大家注意。

Scikit Learn中的多项式回归

在上一节中，我们知道多项式回归其实就是对样本数据进行预处理，然后用线性回归的算法进行模型训练，所以多项式回归的核心在于多样本数据做预处理。那么在Scikit Learn中针对多项式回归的类PolynomialFeatures是在preprocessing包中：

import numpy as np
import matplotlib.pyplot as plt

# 构建样本数据
x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x ** 2 + x + 2 + np.random.normal(0, 1, size=100)

# 导入多项式处理的类
from sklearn.preprocessing import PolynomialFeatures
# degree参数表示将样本数据处理为至少包含有几次幂的特征
poly = PolynomialFeatures(degree=2)
poly.fit(X)
X2 = poly.transform(X)

在实例化PolynomialFeatures时构造函数需要的degree参数表示将样本数据处理为至少包含有几次幂特征的数据。比如degree=2，那么转换后的样本数据中的特征数量至少是2，其中一个是原始的特征，另一个是将原始特征平方后的特征。那么为什么说是至少有两个特征呢，我们来看看上面代码中转换后的X2：

X2.shape
# 结果
(100, 3)

我们看到转换后的样本数据X2是一个100行3列的矩阵，说明通过PolynomialFeatures(degree=2)转换后，我们期望的2个特征变成了3个，我们来看看前5行的样本数据：

X2[:5, :]
# 结果
array([[  1.00000000e+00,  -2.67091119e+00,   7.13376657e+00],
	   [  1.00000000e+00,   9.26429770e-01,   8.58272118e-01],
	   [  1.00000000e+00,   2.19969933e+00,   4.83867715e+00],
	   [  1.00000000e+00,   3.13320069e-01,   9.81694657e-02],
	   [  1.00000000e+00,  -8.02234471e-02,   6.43580146e-03]])

可以看到转换后的第一列相当于是对特征做了0次方，值都是1，第二列是原始特征，第三列是原始特征平方后的特征。然后我们再用线性回归对转换后的样本数据进行处理：

from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(X2, y)
y_predict = lr.predict(X2)

plt.scatter(x, y)
plt.plot(np.sort(x), y_predict[np.argsort(x)], color='r')
plt.show()

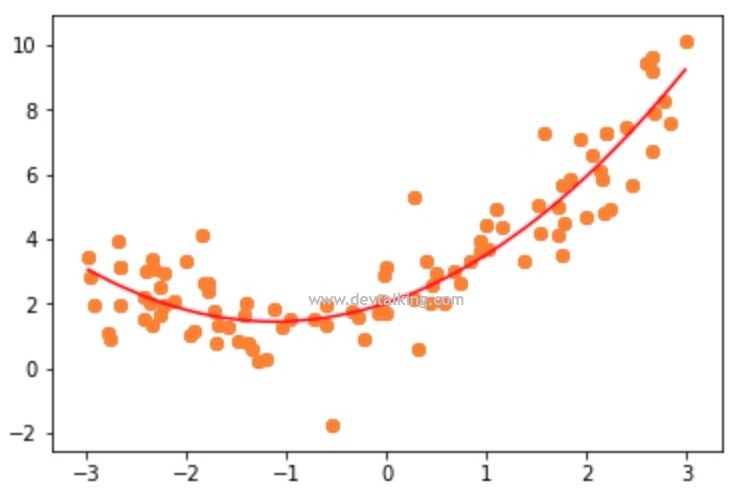
以上就是在Scikit Learn中使用多项式回归的方式。下面我们再来仔细看一下PolynomialFeatures这个类。

# 构造简单的样本数据
X_simple = np.arange(1, 11).reshape(-1, 2)

X_simple
# 结果
array([[ 1,  2],
	   [ 3,  4],
	   [ 5,  6],
	   [ 7,  8],
	   [ 9, 10]])

构造一个简单的样本数据，元素从1到10，一共5行2列，既是一个有两个特征的样本数据，然后使用PolynomialFeatures对这个样本数据进行处理：

poly = PolynomialFeatures(degree=2)
poly.fit(X_simple)
X2_simple = poly.transform(X_simple)

X2_simple
# 结果
array([[   1.,    1.,    2.,    1.,    2.,    4.],
	   [   1.,    3.,    4.,    9.,   12.,   16.],
	   [   1.,    5.,    6.,   25.,   30.,   36.],
	   [   1.,    7.,    8.,   49.,   56.,   64.],
	   [   1.,    9.,   10.,   81.,   90.,  100.]])

我们看到当原始样本数据有2个特征，然后希望转换后的样本数据里增加对每个原始特征进行平方的新特征，通常情况下我们的预期可能是转换后有样本数据有4个特征，2个原始特征，2个对应做了平方处理的新特征。但是实际的情况是转换后的样本数据是一个5行6列的矩阵，既有6个特征的样本数据。

我们来分析一下：

• 第一列全部为1。
• 第二列和第三列是原始特征。
• 第四列和第六列分别是第二列原始特征和第三列原始特征的平方。
• 第五列是第二列原始特征和第三列原始特征的乘积。

我们再来看一下如果将degree参数设置为3，转换后的样本数据会有几个特征：

poly = PolynomialFeatures(degree=3)
poly.fit(X_simple)
X3_simple = poly.transform(X_simple)

X3_simple.shape
# 结果
(5, 10)

如果原始特征为$x_1$和$x_2$，那么X3_simple中10个特征分别为：1，$x_1$，$x_2$，$x_1^2$，$x_2^2$，$x_1x_2$，$x_1^3$，$x_2^3$，$x_1^2x_2$，$x_1x_2^2$。

可见当改变PolynomialFeatures的degree参数后，转换后样本数据的特征会成指数级的增长，它会尽可能的列出所有的多项式来丰富样本数据。

Pipeline

现在我们知道，使用多项回归，首先就是对样本数据进行预处理，但是当degree值比较大的时候，我们的样本数据的特征分布会非常分散，比如1的1次方和100的100次方，这使得样本数据的特征值分布非常不均衡，这会使训练出的模型误差比较大。在第三篇笔记中，我们讲过数据归一化，就是解决这个问题的工具，所以在多项式回归中，数据归一化也是我们经常需要处理的步骤，再然后才是线性回归的处理。

那么整个多项式回归至少就有三个步骤，分别为对样本数据进行多项式的预处理、对样本数据进行归一化、对样本数据进行线性回归处理。对不同的样本数据，每次都要做这三次步骤还是比较繁琐的，所以Scikit Learn给我们提供了一个Pipeline的工具，既可以将若干步骤打包成一个对象，相当于制作一个流程模板，这样面对不同的样本数据，我们只需要处理一次既可，Pipeline内部帮我们处理了打包在里面的其他步骤，极大提高了效率。

# 导入Pipeline和其他需要打包进Pipeline的类
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import PolynomialFeatures

# 封装Pipeline
poly_pipeline = Pipeline([
	("poly", PolynomialFeatures(degree=2)),
	("std_scalar", StandardScaler()),
	("lr", LinearRegression())
])

构建Pipeline的过程就是封装步骤的过程，Pipeline构造函数的参数需要传入一个数组，数组元素的类型为元组，元组的第一个元素为字符串，既标识这一步是做什么事的，第二个元素是处理对应步骤的类。从上面构造的Pipeline可以看出，是将三个步骤进行了打包，第一个步骤的对样本数据进行多项式的预处理，第二个步骤是对样本数据进行归一化，第三个步骤是对样本数据进行线性回归处理。封装好Pipeline后，使用的方式和机器学习的算法保持一致：

poly_pipeline.fit(X, y)
y_predict_pipeline = poly_pipeline.predict(X)

plt.scatter(x, y)
plt.plot(np.sort(x), y_predict_pipeline[np.argsort(x)], color='r')
plt.show()

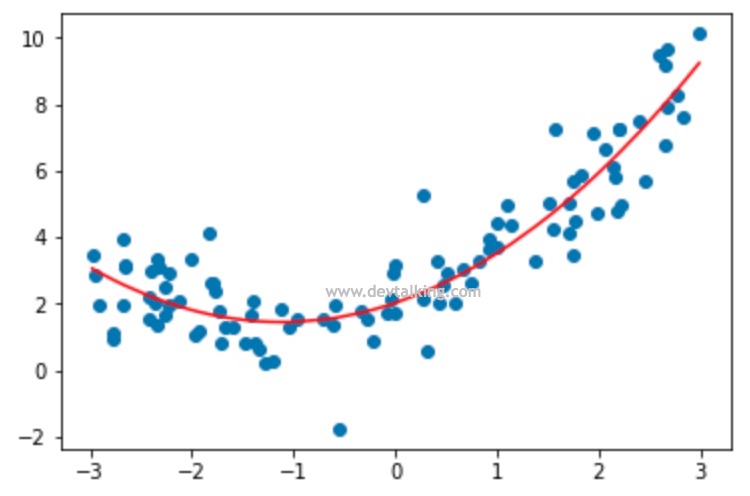
可以看到最终的结果和我们之前将每一步单独分开得到的结果相同。在实际处理多步骤、复杂的机器学习问题时，Pipeline非常有用，是很好的化繁为简的工具。

欠拟合和过拟合

在讲欠拟合和过拟合前，我们先来回顾一下线性回归的评测标准均方误差（MSE）：

$$ \frac 1 m \sum_{i=1}^m(y_{test}^{(i)} - \hat y_{test}^{(i)})^2$$

就是将原始目标值和通过模型计算出的目标值相减再平方，这就是其中一条样本数据的误差，将所有样本数据的误差相加再除以所有样本数据的数量，就得到了均方误差。均方误差值约小说明训练出的模型越好，也就是拟合的越好，反之亦然。其实欠拟合和过拟合从字面上也很好理解，前者表示拟合程度不够，通过模型计算出的目标值与原始目标值差距太大，后者表示拟合程度过高，以至于无法表示出样本数据的共性和真实情况。下面我们来看看示例：

import numpy as np
import matplotlib.pyplot as plt

# 构建样本数据
x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x ** 2 + x + 2 + np.random.normal(0, 1, size=100)

# 先用线性回归进行拟合
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(X, y)
y_predict = lr.predict(X)

# 导入均方误差
from sklearn.metrics import mean_squared_error
mean_squared_error(y, y_predict)
# 结果
2.6823097152963338

我们构建和之前一样的样本数据，然后先使用线性回归训练模型，然后通过模型计算出的值的均方误差为2.68。然后再用多项式回归对同样的样本数据训练模型看看结果：

# 这里用到上节讲到的Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

def PolynomialRegression(degree):
	return Pipeline([
		("poly", PolynomialFeatures(degree=degree)),
		("std_scalar", StandardScaler()),
		("lr", LinearRegression())
	])
	
poly2_reg = PolynomialRegression(degree=2)
poly2_reg.fit(X, y)
y2_predict = poly2_reg.predict(X)

mean_squared_error(y, y2_predict)
# 结果
0.93160950356090177

可以看到使用多项式回归方式训练出的模型计算出的目标值与原始目标值的均方误差只有0.93，说明拟合程度要远远好与用线性回归训练的模型。那么如果在对样本数据进行预处理时进一步增加多项式特征，MSE会有变化吗？我们来看一下：

poly5_reg = PolynomialRegression(degree=5)
poly5_reg.fit(X, y)
y5_predict = poly5_reg.predict(X)

mean_squared_error(y, y5_predict)
# 结果
0.91189515020672107

从结果看到，当增加样本数据的多项式特征后，MSE是逐渐变小的，既多项式特征维度越高，MSE越小。

poly100_reg = PolynomialRegression(degree=100)
poly100_reg.fit(X, y)
y100_predict = poly100_reg.predict(X)

mean_squared_error(y, y100_predict)
# 结果
0.4885145394655237

当将PolynomialRegression的degree设为100时，MSE已经缩小到0.488了。那么是不是预处理后的样本数据中特征越多就越好呢？我们先将degree=100时的拟合曲线绘制出来看看：

plt.scatter(x, y)
plt.plot(np.sort(x), y100_predict[np.argsort(x)], color='r')
plt.show()

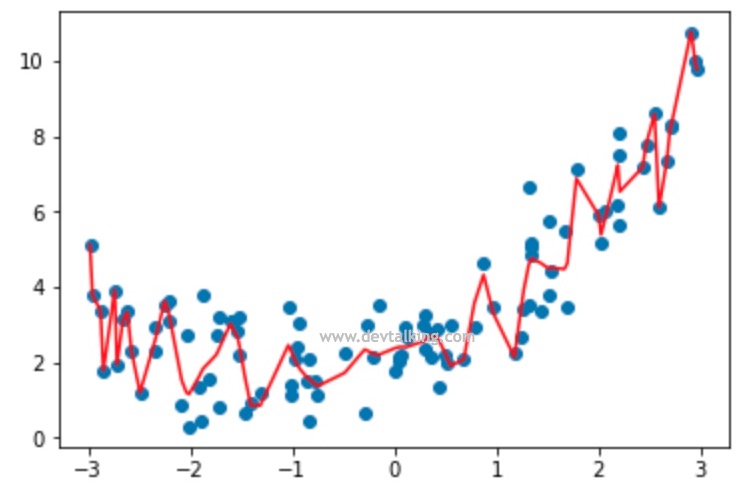
可以看到这根曲线的弯曲程度已经非常复杂了，如果degree取足够高的值的话，是可以求出一条经过所有点的曲线的，既MSE为0，那条线基本就是将所有点连接起来的线，其复杂程度可想而知。那么就上面这根曲线来看，有很多断崖式的下降，对于这些局部下降的曲线来看其实拟合程度是非常不好的，虽然整体曲线呈上升趋势，但是有太多的局部拟合不好的地方，所以虽然MSE比较小，但是这条曲线并不是一条很好的拟合曲线，这就是过拟合。

另外，因为我们的样本数据构建的是一组随机数据，并且在计算$y$的方程中增加了噪音，所以上面曲线有很多地方并没有点，我们再构造一个连续的样本数据来看看经过degree=100后，绘制的曲线是什么样的：

# 绘制从-3到3连续的100个点，然后将其转换为100行1列的矩阵，既我们新的样本数据
X_plot = np.linspace(-3, 3, 100).reshape(100, 1)
# 使用我们之前degree参数为100时训练出的多项式回归模型来预测新的样本数据的目标值
y_plot = poly100_reg.predict(X_plot)

# 绘制样本数据点和目标值，并将座标系设置在-3到3的横轴和-1到10的纵轴
plt.scatter(x, y)
plt.plot(X_plot[:, 0], y_plot, color='r')
plt.axis([-3, 3, -1, 10])
plt.show()

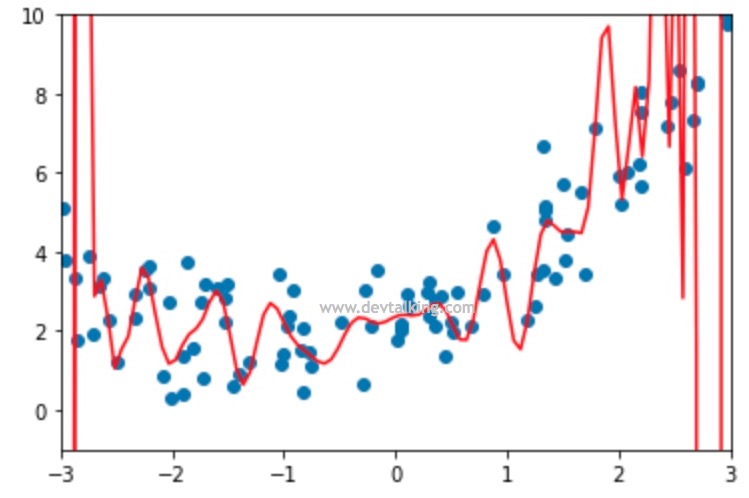
我们看到，这时我们曲线波动的更加厉害，尤其曲线两端，所以很明显这条曲线不是一条很好的拟合曲线。

模型泛化

其实在我们实际运用中，通常解决的都是过拟合的问题，这里我们再用数据来阐述一下过拟合问题。在第三篇笔记中，我们讲过对样本数据进行拆分，按一定比例分为训练数据和测试数据，目的在于验证训练出的模型预测训练数据以外的数据的准确性，继而评判模型的好坏。那么对于上面例子中，当degree的值为100时，MSE确实很小，但只是针对训练数据，也就是说这个模型在预测有限的、已知的训练数据而言，准确率很高。但是当这个模型在训练其他样本数据时准确率却很差，这就是典型的过拟合的特征，这也引出了一个概念，那就是泛化模型，这个概念很好理解，一个好的模型，应该具有普适性，对于数据特征类似的不同的样本数据应该都有比较好的预测准确率，说明泛化性比较好，上一节训练出的多项回归模型显然就是一个泛化性不好的模型。下面我们用数据再来验证一下：

# 导入拆分样本数据为训练数据和测试数据的方法
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y)
X_train.shape
# 结果
(75, 1)

X_test.shape
# 结果
(25, 1)

# 用degree为100的PolynomialFeatures通过训练数据训练模型
poly100_reg.fit(X_train, y_train)
# 使用训练出的模型对训练特征数据预测训练目标值
y100_predict_train = poly100_reg.predict(X_train)
# 求均方误差
mean_squared_error(y_train, y100_predict_train)
# 结果
0.31894921748706134

可以看到，对于范围有限、已知的训练数据X_train而言，训练出的模型预测结果还是比较好的，MSE只有0.32。那我们再来看看用同样的模型来预测测试数据，结果会怎样：

y100_predict_test = poly100_reg.predict(X_test)
mean_squared_error(y_test, y100_predict_test)
# 结果
223782770464.89853

可以看到MSE都上亿了，足以可见这个模型的泛化性非常差。如果我们使用degree=2来预处理数据，看看训练出的模型的泛化性怎么样：

poly2_reg.fit(X_train, y_train)
y2_predict_train = poly2_reg.predict(X_train)
mean_squared_error(y_train, y2_predict_train)
# 结果
1.0237070125963763

y2_predict_test = poly2_reg.predict(X_test)
mean_squared_error(y_test, y2_predict_test)
# 结果
0.87695907380413585

从上面的结果可以看到，poly2_reg的模型泛化性非常好，预测测试数据的MSE甚至比预测训练数据的MSE还要小。

申明：本文为慕课网liuyubobobo老师《Python3入门机器学习 经典算法与应用》课程的学习笔记，未经允许不得转载。