SVM处理非线性问题

我们在 机器学习笔记八之多项式回归、拟合程度、模型泛化 中讲过线性回归通过多项式回归方法处理非线性问题，同样SVM也可以使用多项式方法处理非线性问题。

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

# 使用datasets提供的方法构建非线性数据
X, y = datasets.make_moons()

我们可以使用datasets提供的make_moons()函数生成非线性数据，默认为100行2列的矩阵，既100个样本数据，每个样本数据2个特征。可以使用n_samples参数指定样本数据数量。我们将其绘制出来看看：

plt.scatter(X[y==0, 0], X[y==0, 1])
plt.scatter(X[y==1, 0], X[y==1, 1])
plt.show()

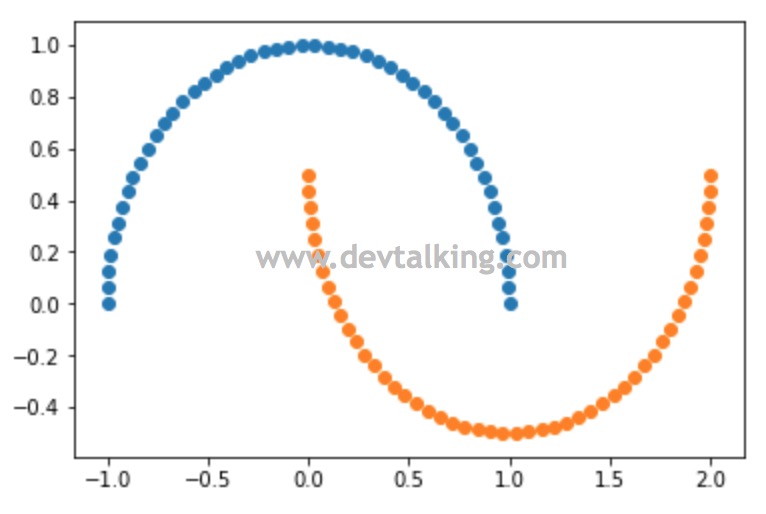
可以看到make_moons()默认生成的数据绘制出的图像是两个规整的半月牙曲线。但是作为样本数据有点太规整了，所以我们可以使用noise参数给生成的数据增加一点噪音：

X, y = datasets.make_moons(noise=0.15)

plt.scatter(X[y==0, 0], X[y==0, 1])
plt.scatter(X[y==1, 0], X[y==1, 1])
plt.show()

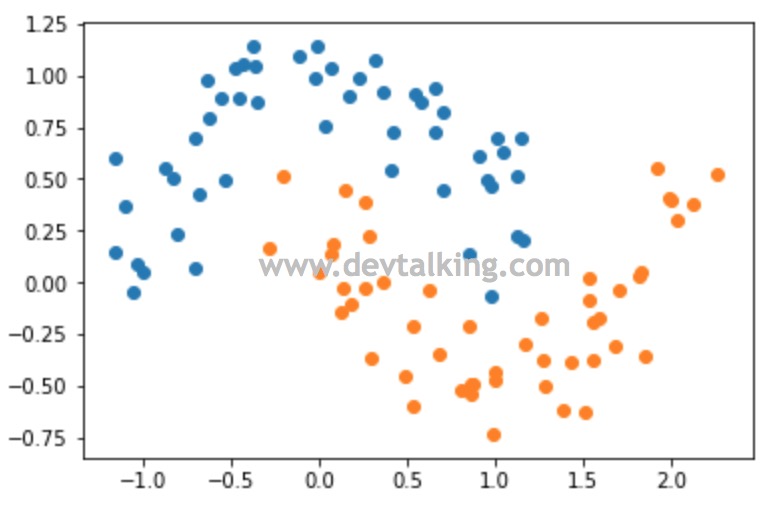
可以看到，增加了噪音后虽然数据点较之前的分布分散随机了许多，但整体仍然是两个半月牙形状。下面我们就在SVM的基础上使用多项式来看看对这个样本数据决策边界的计算：

from sklearn.preprocessing import PolynomialFeatures, StandardScaler
from sklearn.svm import LinearSVC
from sklearn.pipeline import Pipeline

首先我们需要引入我们用到的几个类：

• 多项式自然要用到之前讲过的PolynomialFeatures类。
• 数据归一化需要用到StandardScaler类。
• 同样需要用到Pipeline将多个过程封装在一个函数里，所以要用到Pipeline类。

这一篇笔记主要讲机器学习算法中一个重要的分类算法，支撑向量机（Support Vector Machine）。它背后有严格的数学理论和统计学理论支撑的，这里我们只对它的原理和应用做以介绍，更深层次的数学理论有兴趣可以查阅其他资料。

什么是SVM

上面的图展示的是一个二分类问题，在逻辑回归的笔记中，我们知道了决策边界，图中橘黄色的直线就是决策边界，它看似很好的将样本数据的不同分类区分开了。我们在多项式回归的笔记中，讲过模型泛化的问题，一个模型的好坏程度很大程度上是体现了模型泛化能力的好坏，也就是对未知样本的预测能力。

如果新来一个样本数据A，按照决策边界划分它是被分为了蓝色分类，可事实真的是如此吗，因为点A和红色分类的点非常近，很有可能点A是属于红色分类的。所以上图中的决策边界可能并不是最优的，那最优的决策边界应该是什么样的呢？

上面的决策边界之所以有缺陷，是因为它和红色类别的点太近了，当然肯定也不能和蓝色的点太近了，所以我们希望这条决策边界离红色分类和蓝色分类都尽可能的远，才能很好的避免上面出现的问题。

想要决策边界离红蓝两个分类都尽可能的远，也就是红蓝分类两边离决策边界最近的点的距离要远，并且两边的点到决策边界的距离要相等，这才说明决策边界是不偏不倚的，如上图所示。

过红蓝两边离决策边界最近的点画两条直线，并且平行于决策边界，那么就确定了一个区域，在这个区域内不应该再有任何数据点出现。那么SVM就是尝试寻找这个区域中间那条最优的决策边界。这个区域边界上的点称为支撑向量，换句话说，是支撑向量定义出了这个区域，那么最优的决策边界也是由支撑向量决定的，这也是支撑向量机这个名称的由来。

如上图所示，由支撑向量确定的区域之间的距离称为Margin。那么SVM要做的事情就是最大化Margin，既将问题转化为了求最优解的问题。

以上对SVM的解释是基于线性可分问题的基础上，也就是能确确实实找到一条直线作为决策边界，这种问题称为Hard Margin SVM，但是很多真实的情况是线性不可分的，这类问题称为Soft Margin SVM，这两类问题都是支撑向量机可以处理的，但基础还是Hard Margin SVM。

机器学习算法中有一个重要环节就是评判算法的好坏，我们在之间的笔记中讲过多种评价回归算法的评测标准，比如均方误差（MSE）、均方根误差（RMSE）、平均绝对误差（MAE）、$R^2$（R Squared）。但是在分类问题中我们一直使用分类准确度这一个指标，也就是预测对分类的样本数量除以总预测样本数量。但是这个方法存在很大的一个缺陷，所以这篇笔记主要介绍评价分类问题的方式方法。

极度偏斜数据（Skewed Data）

为什么说分类准确度这个指标存在很大的一个缺陷呢。举个例子，假设有一个癌症预测系统，输入体检信息，判断是否患有癌症。我们知道世界上相对于其他病症，患癌症的比例还是很小，如果癌症产生的概率只有0.1%，那么有99.9%的人都不会患有癌症。这就意味着，就算癌症预测系统什么都不做，但凡有体检信息输入，就给出没有患癌症的结果，那准确率也是达到了99.9%。那此时这个分类准确度是真实的吗？所以当样本数据或领域的实际情况存在数据极度偏斜的时候，只使用分类准确度这个指标是远远不够的。

混淆矩阵（Confusion Matrix）

这一节介绍一个能进一步分析分类结果的工具，混淆矩阵。

上面这个表针对二分类问题，所有将类别就分为两类0和1，0表示Negative，类似医院上的阴性，1表示Positive，类似医学上的阳性。行代表真实值，列代表预测值。

如上图所示：

• (0, 0)格子真实值和预测值都为0，称为预测Negative正确，记作True Negative，简写为TN。
• (0, 1)格子真实值为0，但预测值为1，称为预测Positive错误，记作False Positive，简写为FP。
• (1, 0)格子真实值为1， 但预测值为0，称为预测Negative错误，记作False Negative，简写为FN。
• (1, 1)格子真实值和预测值都为1，称为预测Positive正确，记作True Positive，简写为TP。

以上这个表格就叫做混淆矩阵。举个例子，如果对10000个人预测他们是否患癌症，通过混淆矩阵表示出的真实情况就是：

解读一下：

• 没有患癌症，系统也预测出没有患癌症的人为9978人（TN）。
• 没有患癌症，但系统预测出患癌症的人为12人（FP）。
• 患有癌症，但系统预测出没有患癌症的人为2人（FN）。
• 患有癌症，系统也预测出患有癌症的人为8人（TP）。

OmniFocus的几个主要概念

文章中所有的内容都是以OmniFocus 3为例。

• 文件夹：OmniFocus中任务的组织结构最顶级一层，但只是用于分类，本身没有什么属性。
• 项目：顾名思义，用于定义我们生活和工作中大大小小的项目，项目本身也有属性设置，可设置标签、其内任务的关系（并行、串行、单个），截止日期等。项目下可包含多个任务。
• 任务：OmniFocus中承载事件的最小颗粒。因为OmniFocus支持任务无限嵌套，所以当多个任务在一个任务下时该任务就成为一个任务组。
• 任务组：任务组本身也是一个任务，但是它又是其他任务的父任务，所以任务组有子任务关系（并行、串行、单个）的设置。
• 标签：任务、项目身上都可以设置一到多个标签。标签可以嵌套，并且标签支持设置地理位置，并且有根据进入，走出两个行为和距离范围设置通知。
• 透视：根据各种条件筛选任务的视图。比如查看有标签“办公室”，即将截至的任务。条件可以按照包含任意、全部包含和不包含进行组合。然后还可以设置筛选出来任务的排列、分组方式。

任务系统

我参照John Z. Sonmez的看板+番茄钟的系统，将其调整为OmniFocus+番茄钟的系统。

系统设置

• 在截止日期这一项，将即将截止日期的表示设置为今天。
• 今天和Watch这一项，设置为自定义透视的今日（该透视下面会讲到）。

构建系统的主要标签

• 仪式：周期性重复的任务会设置该标签。
• 地点：标明某个任务能在何种场所进行。
  • 办公室
  • 家
  • 通勤中
• 状态：进行任务时需要投入的专注度。
  • 集中精力
  • 放松
• 跟踪：需要跟踪的任务会设置该标签，比如安排下去的任务需要在某个时间点知道完成的结果。
• 采购：需要购买东西的任务会设置该标签。
• 星期：规划一周任务时设置的标签。
  • 周一
  • 周二
  • 周三
  • 周四
  • 周五
  • 周六
  • 周日
• 二分钟：能在很短时间内完成的任务会设置该标签。

决策边界

决策边界顾名思义就是需要分类的数据中，区分不同类别的边界，举个不恰当的例子，就像省的地界一样，你处在北京还是处在河北，全看你站在区分北京和河北的那条线的哪边。这节我们来看看使用逻辑回归算法如何绘制鸢尾花前两个分类的决策边界。

线性决策边界

再来回顾一下逻辑回归，我们需要找到一组$\theta$值，让这组$\theta$和训练数据相乘，然后代入Sigmoid函数，求出某个类别的概率，并且假设，当概率大于等于0.5时，分类为1，当概率小于0.5时，分类为0：

$$\hat p = \sigma(\theta^T X_b)=\frac 1 {1+e^{-\theta^{T}X_b}}$$

$$\hat y =\left\{
\begin{aligned}
1, \ \ \ \hat p \ge 0.5 \\
0, \ \ \ \hat p < 0.5 \\
\end{aligned}
\right.
$$

在Sigmoid函数那节解释过，当$t>0$时，$\hat p>0.5$。当$t<0$时，$\hat p<0.5$，因为$t= \theta^T X_b $，所以：

$$\hat y =\left\{
\begin{aligned}
1, \ \ \ \ \hat p \ge 0.5, \ \ \ \ \theta^T X_b \ge 0 \\
0, \ \ \ \ \hat p < 0.5, \ \ \ \ \theta^T X_b < 0 \\
\end{aligned}
\right.
$$

那么当$\theta^T X_b =0$时，理论上$\hat p$就是0.5，分类既可以为0，也可以为1。只不过我们在这里将$\hat p=0.5$是，分类假设为1。由此可见$\theta^T X_b =0$就是逻辑回归中的决策边界，并且是线性决策边界。