机器学习笔记十四之核函数（Kernel Function）

SVM处理非线性问题

我们在 机器学习笔记八之多项式回归、拟合程度、模型泛化 中讲过线性回归通过多项式回归方法处理非线性问题，同样SVM也可以使用多项式方法处理非线性问题。

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

# 使用datasets提供的方法构建非线性数据
X, y = datasets.make_moons()

我们可以使用datasets提供的make_moons()函数生成非线性数据，默认为100行2列的矩阵，既100个样本数据，每个样本数据2个特征。可以使用n_samples参数指定样本数据数量。我们将其绘制出来看看：

plt.scatter(X[y==0, 0], X[y==0, 1])
plt.scatter(X[y==1, 0], X[y==1, 1])
plt.show()

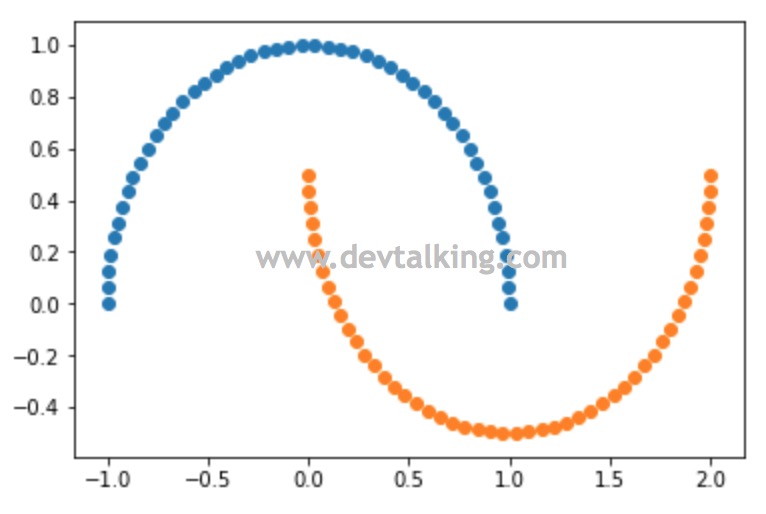
可以看到make_moons()默认生成的数据绘制出的图像是两个规整的半月牙曲线。但是作为样本数据有点太规整了，所以我们可以使用noise参数给生成的数据增加一点噪音：

X, y = datasets.make_moons(noise=0.15)

plt.scatter(X[y==0, 0], X[y==0, 1])
plt.scatter(X[y==1, 0], X[y==1, 1])
plt.show()

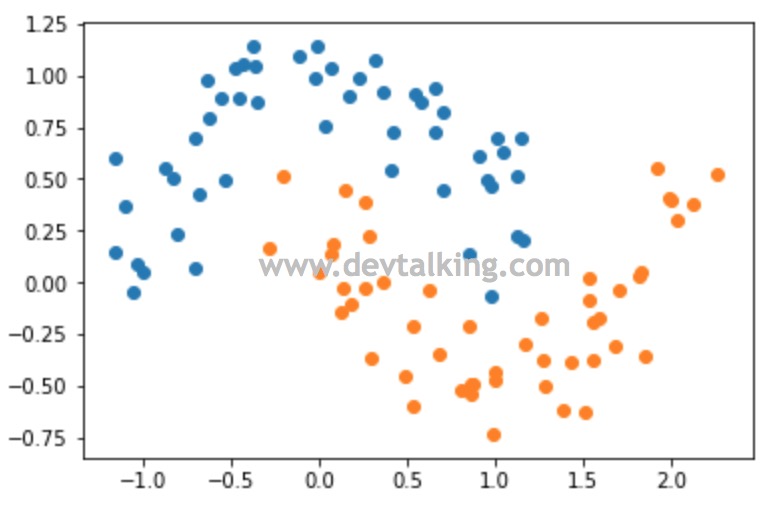
可以看到，增加了噪音后虽然数据点较之前的分布分散随机了许多，但整体仍然是两个半月牙形状。下面我们就在SVM的基础上使用多项式来看看对这个样本数据决策边界的计算：

from sklearn.preprocessing import PolynomialFeatures, StandardScaler
from sklearn.svm import LinearSVC
from sklearn.pipeline import Pipeline

首先我们需要引入我们用到的几个类：

• 多项式自然要用到之前讲过的PolynomialFeatures类。
• 数据归一化需要用到StandardScaler类。
• 同样需要用到Pipeline将多个过程封装在一个函数里，所以要用到Pipeline类。

# 定义多项式SVM函数
def PolynomialSVC(degree, C=1.0):
	return Pipeline([
		("poly", PolynomialFeatures(degree=degree)),
		("std_scaler", StandardScaler()),
		("linearSVC", LinearSVC(C=C))
	])

# 使用多项式SVM训练样本数据
ploy_svc = PolynomialSVC(degree=3)
ploy_svc.fit(X, y)

def plot_decision_boundary(model, axis):
	# meshgrid函数用两个坐标轴上的点在平面上画格，返回坐标矩阵
	X0, X1 = np.meshgrid(
		# 随机两组数，起始值和密度由坐标轴的起始值决定
		np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
		np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1),
	)
	# ravel()方法将高维数组降为一维数组，c_[]将两个数组以列的形式拼接起来，形成矩阵
	X_grid_matrix = np.c_[X0.ravel(), X1.ravel()]
	
	# 通过训练好的逻辑回归模型，预测平面上这些点的分类
	y_predict = model.predict(X_grid_matrix)
	y_predict_matrix = y_predict.reshape(X0.shape)
	
	# 设置色彩表
	from matplotlib.colors import ListedColormap
	my_colormap = ListedColormap(['#0000CD', '#40E0D0', '#FFFF00'])
	
	# 绘制等高线，并且填充等高区域的颜色
	plt.contourf(X0, X1, y_predict_matrix, linewidth=5, cmap=my_colormap)

plot_decision_boundary(ploy_svc, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y==0, 0], X[y==0, 1])
plt.scatter(X[y==1, 0], X[y==1, 1])
plt.show()

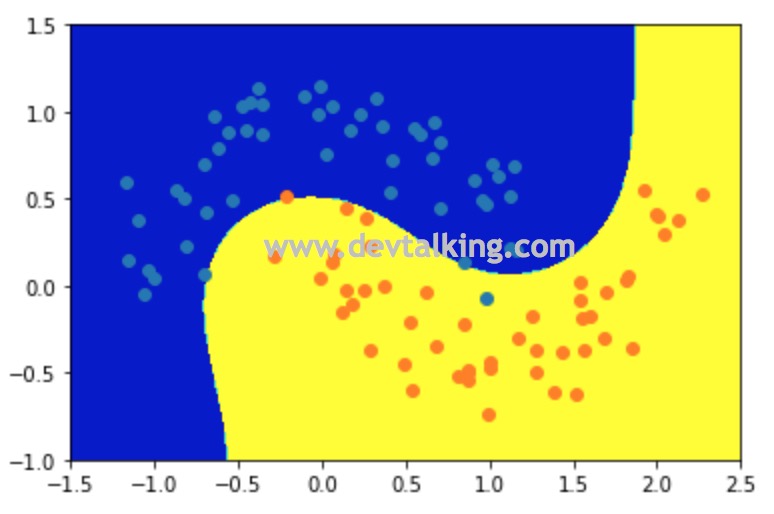
从上图可以看到决策边界的情况，很明显已经不是线性决策边界了，并且能较好的将两类点区分开。

核函数（Kernel Function）

核函数是机器学习算法中一个重要的概念。简单来讲，核函数就是样本数据点的转换函数。之所以在SVM这篇笔记中介绍核函数，是因为在SVM处理非线性的问题中除了上一节介绍的方法外，还有使用核函数的方式。而介绍核函数的切入点也是通过多项式这个知识点来讲的。

什么是核函数

首先我们回顾一下多项式方法。对样本数据进行多项式转换并不是真正的增加了样本数据的特征数量，而且对原有的特征数据进行转换，构造出其他特征，这些新构造出的特征和原始特征都有强关联。

比如如果将原本只有$x_1$、$x_2$两个特征的样本数据通过多项式转换为有10个特征的数据，那么转换后的这10个特征分别为：1，$x_1$，$x_2$，$x_1^2$，$x_2^2$，$x_1x_2$，$x_1^3$，$x_2^3$，$x_1^2x_2$，$x_1x_2^2$。

假设某个机器学习算法的原始公式中含有$x_ix_j$（$x_i $和$x_j$为特征向量），如果是使用多项式的方法，那么首先需要将$x_i$和$x_j$转换为$x’_i$和$x’_j$，然后转换后的，具有10个元素的两个新特征向量再相乘。如果转换后的特征数量比较多的时候，新特征向量的计算复杂度就会变的很高，并且还需要占用大量内存在存储庞大的特征向量。

那么核函数就是要解决上面的问题。所以多项式核函数就是有这样一个函数，将$x_i$和$x_j$作为参数传入，再指定要构造的特征数，然后该函数直接返回$x’_ix’_j$的值。该函数既可以模拟多项式构造特征的原理，又能将新特征向量的点乘计算出来，同时计算复杂度相对比较小，而且也不用存储庞大的新特征向量。

下面就来看看多项式核函数：

$$K(x,y)=(x \cdot y + 1)^2$$

我们将上面的公式展开来看看：

$$K(x,y)=(\sum_{i=1}^nx_iy_i + 1)$$

应用任意次项和的展开式公式，上面的公式继续展开后得：

$$K(x,y)=\sum_{i=1}^n(x_i^2)(y_i^2) + \sum_{i=2}^n\sum_{j=1}^{i-1}(\sqrt 2 x_ix_j)(\sqrt 2 y_iy_j) + \sum_{i=1}^n(\sqrt 2x_i)(\sqrt 2y_i) + 1$$

上面的公式我们就可以看做是若干项相乘再相加，对于$x$来说：

• 从$\sum_{i=1}^n(x_i^2)(y_i^2)$可以分析出共有$(x_n^2,…,x_1^2)$这么多项。
• 从$\sum_{i=2}^n\sum_{j=1}^{i-1}(\sqrt 2 x_ix_j)(\sqrt 2 y_iy_j)$可以分析出共有$(\sqrt 2x_nx_{n-1},…,\sqrt 2x_2x_1)$这么多项。
• 从$\sum_{i=1}^n(\sqrt 2x_i)(\sqrt 2y_i)$可以分析出共有$(\sqrt 2x_n,…,\sqrt 2x_1)$

将上面的三个向量合起来其实就相当于将原始$x$特征向量根据多项式原理转换后的新的特征向量$x’$：

$$x’= (x_n^2,…,x_1^2,\sqrt 2x_nx_{n-1},…,\sqrt 2x_2x_1,\sqrt 2x_n,…,\sqrt 2x_1,1)$$

根据同样的道理，也可以得出新的$y’$。所以将$K(x,y)$展开后的公式就相当于$x’ \cdot y’$。

综上多项式核函数的公式为：

$$K(x,y) = (x \cdot y + c)^d$$

$d$ 代表多项式中的degree，$c$代表Soft Margin SVM中的$C$，是两个超参数。

以上是通过多项式核函数解释核函数的概念和数学原理，那么不同的机器学习算法里有很多不同的核函数，对应对原始样本数据不同的转换。

通过核函数方式使SVM处理非线性问题

我们再回过头来看看SVM解决非线性的问题，之前我们使用常规的多项式方法，这节我们来看看如何使用核函数：

from sklearn.svm import SVC
def PolynomailKernelSVC(degree, C=1):
	return Pipeline([
		("std_scaler", StandardScaler()),
		("kernelSVC", SVC(kernel="poly", degree=degree, C=C))
	])

poly_kernel_svc = PolynomailKernelSVC(degree=3)
poly_kernel_svc.fit(X, y)

plot_decision_boundary(poly_kernel_svc, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y==0, 0], X[y==0, 1])
plt.scatter(X[y==1, 0], X[y==1, 1])
plt.show()

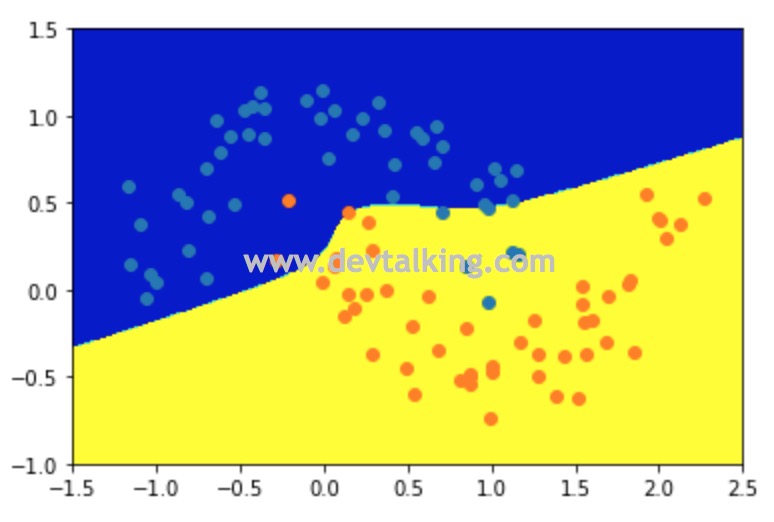
Scikit Learn中使用了多项式核函数的SVM的类是SVC，它的kernel参数就表示要使用哪种核函数，上面示例中传入的poly就表示多项式核函数。

高斯核函数

这一节我们来看看应用非常广泛的一个核函数，高斯核函数。它的名称比较多，以下名称指的都是高斯核函数：

• 高斯核函数。
• RBF（Radial Basis Function Kernel）。
• 径向基函数。

对于多项式核函数而言，它的核心思想是将样本数据进行升维，从而使得原本线性不可分的数据线性可分。那么高斯核函数的核心思想是将每一个样本点映射到一个无穷维的特征空间，从而使得原本线性不可分的数据线性可分。

我们先来回顾一下多项式特征，如下图所示，有一组一维数据，两个类别，明显是线性不可分的情况：

然后通过多项式将样本数据再增加一个维度，假设就是$x^2$，样本数据就变成这样了：

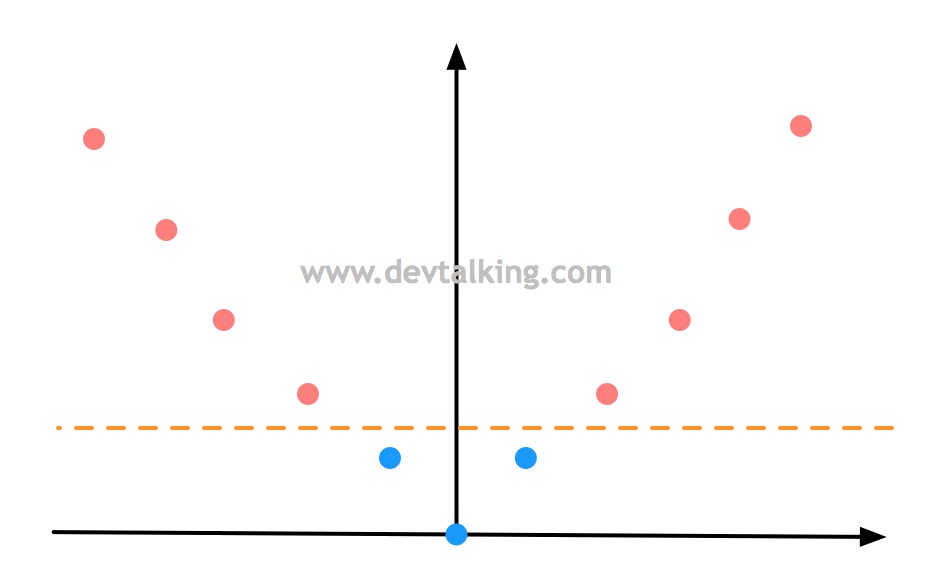
此时原本线性不可分的样本数据，通过增加一个维度后就变成线性可分的状态。这就是多项式升维的意义。

下面我们先来认识一下高斯核函数的公式：

$$K(x, y) = e^{-\gamma||x-y||^2}$$

上面公式中的$\gamma$就是高斯核函数的超参数。然后我们再来看看高斯核函数使线性不可分的数据线性可分的原理。

为了方便可视化，我们将高斯核函数中的$y$取两个定值$l_1$核$l_2$，这类点称为地标（Land Mark）。那么高斯核函数升维过程就是假如有两个地标点，那么就将样本数据转换为二维，也就是将原本的每个$x$值通过高斯核函数和地标，将其转换为2个值，既：

$$x \to (e^{-\gamma||x-l_1||^2}, e^{-\gamma||x-l_2||^2})$$

下面我们用程序来实践一下这个过程：

import numpy as np
import matplotlib.pyplot as plt

# 构建样本数据，x值从-4到5，每个数间隔为1
x = np.arange(-4, 5, 1)
x

# 结果
array([-4, -3, -2, -1,  0,  1,  2,  3,  4])

# y构建为0，1向量，且是线性不可分的
y = np.array((x >= -2) & (x <= 2), dtype='int')
y

# 结果
array([0, 0, 1, 1, 1, 1, 1, 0, 0])

# 绘制样本数据
plt.scatter(x[y==0], [0]*len(x[y==0]))
plt.scatter(x[y==1], [0]*len(x[y==1]))
plt.show()

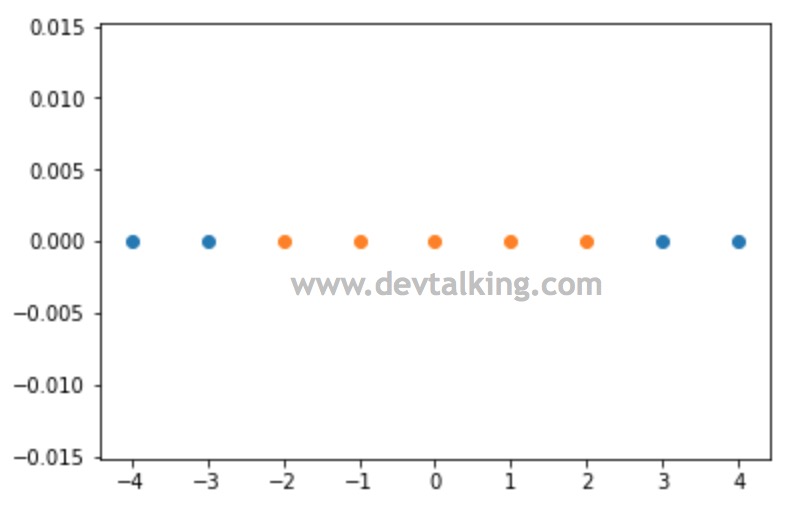
可以看到我们构建的样本数据是明显线性不可分的状态。下面我们来定义高斯核函数：

def gaussian(x, l):
	# 这一节对gamma先不做探讨，先定为1
	gamma = 1.0
	# 这里x-l是一个数，不是向量，所以不需要取模
	return np.exp(-gamma * (x - l)**2)

# 将每一个x值通过高斯核函数和l1，l2地标转换为2个值，构建成新的样本数据
l1, l2 = -1, 1
X_new = np.empty((len(x), 2))
for i, data in enumerate(x):
	X_new[i, 0] = gaussian(data, l1)
	X_new[i, 1] = gaussian(data, l2)

# 绘制新的样本点
plt.scatter(X_new[y==0, 0], X_new[y==0, 1])
plt.scatter(X_new[y==1, 0], X_new[y==1, 1])
plt.show()

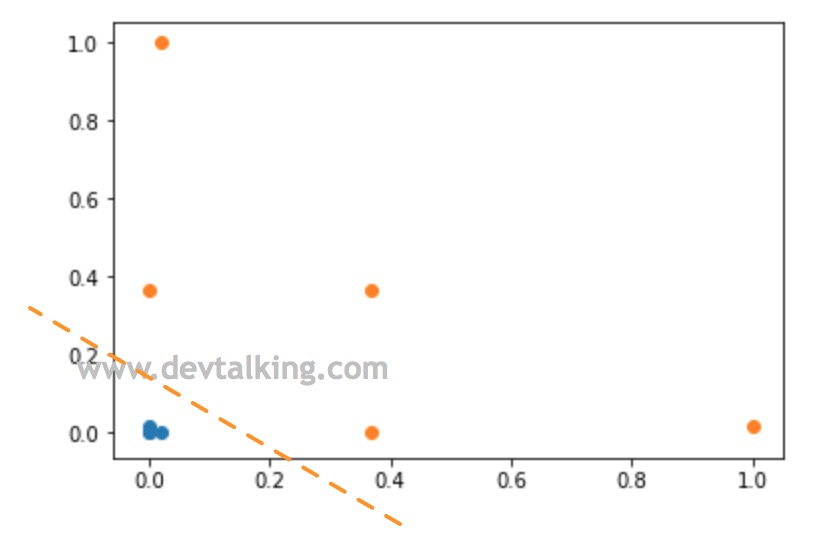
可以看到通过高斯函数将原本的一维样本数据转换为二维后，新样本数据明显成为线性可分的状态。

上面的示例中，我们将高斯核函数中的$y$取定了两个值$l_1$和$l_2$。在实际运用中，是需要真实的将每个$y$值带进去的，也就是每一个样本数据中的$y$都是一个地标，那么可想而知，原始样本数据的行数就是新样本数据的维数，既原始$m*n$的样本数据通过高斯核函数转换后成为$m*m$的数据。当样本数据行数非常多的话，转换后的新样本数据维度自然会非常高，这也就是为什么在这节开头会说高斯核函数的核心思想是将每一个样本点映射到一个无穷维的特征空间的原因。

高斯核函数中的Gamma

在看高斯核函数中的$\gamma$之前，我们先来探讨一个问题，我们以前有学过正态分布，它是一个非常常见的连续概率分布，最关键的是它又名高斯分布，我们再来看看高斯分布的函数：

$$f(x) = \frac 1 {\sigma \sqrt {2 \pi}} e^{-\frac {(x-\mu)^2} {2\sigma^2}}$$

仔细看这个函数就能发现，它和高斯核函数的公式在形态上是一致的：

• 高斯函数$e$前的系数是$\frac 1 {\sigma \sqrt {2 \pi}} $，$e$指数的系数是$-\frac 1 {2\sigma^2}$。
• 高斯核函数$e$前的系数是1，$e$指数的系数是$-\gamma$。

所以高斯核函数的曲线其实也是一个高斯分布图。

下面再来看看高斯分布图以及$\mu$和$\sigma$对分布图的影响：

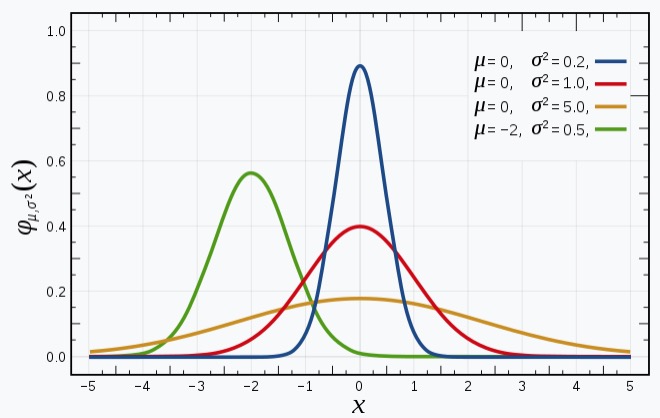
上图是维基百科对高斯分布解释中的分布图，从图中可以看到：

• 高斯分布曲线的形状都是相似的钟形图。
• $\mu$决定分布图中心的偏移情况。
• $\sigma$决定分布图峰值的高低，或者说钟形的胖瘦程度。

因为高斯函数中的$\sigma$和高斯核函数中$\gamma$成倒数关系。所以：

• 高斯函数中$\sigma$越大、高斯分布峰值越小。$\sigma$越小、高斯分布峰值越大。
• 高斯核函数中$\gamma$越大、高斯分布峰值越大，既钟形越窄。$\gamma$越小、高斯分布峰值越小，既钟形越宽。

Scikit Learn中的RBF SVM

这一小节来看看如果使用Scikit Learn中封装的RBF SVM。首先还是先构建样本数据，我们使用和多项式SVM相同的数据：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

X, y = datasets.make_moons(noise=0.15, random_state=666)

plt.scatter(X[y==0, 0], X[y==0, 1])
plt.scatter(X[y==1, 0], X[y==1, 1])
plt.show()

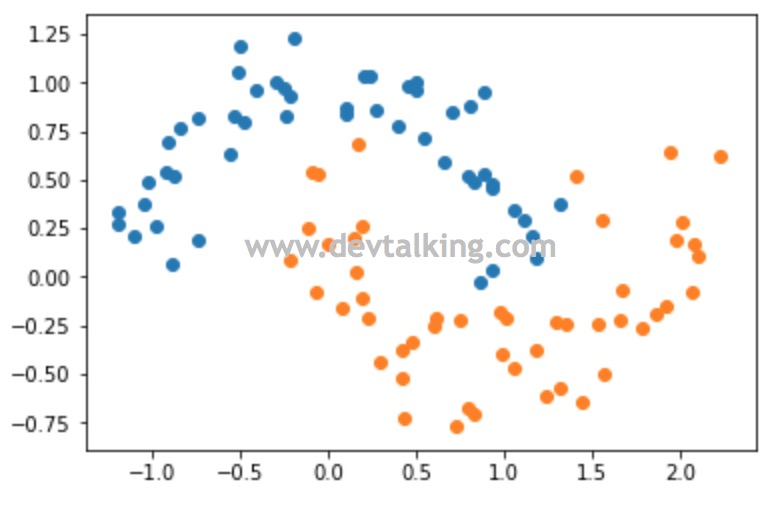
然后通过RBF SVM训练数据并绘制决策边界：

from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.pipeline import Pipeline

def RBFKernelSVC(gamma = 1.0):
	return Pipeline([
		("std_scaler", StandardScaler()),
		("svc", SVC(kernel="rbf", gamma=gamma))
	])

rbf_svc = RBFKernelSVC(gamma=1)
rbf_svc.fit(X, y)

使用RBF SVM和使用多项式SVM其实基本一样，只是将SVC中的kernel参数由之前的poly变更为rbf，然后传入该核函数需要的超参数既可。

接下来绘制决策边界：

def plot_decision_boundary(model, axis):
	# meshgrid函数用两个坐标轴上的点在平面上画格，返回坐标矩阵
	X0, X1 = np.meshgrid(
		# 随机两组数，起始值和密度由坐标轴的起始值决定
		np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),
		np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1),
	)
	# ravel()方法将高维数组降为一维数组，c_[]将两个数组以列的形式拼接起来，形成矩阵
	X_grid_matrix = np.c_[X0.ravel(), X1.ravel()]
	
	# 通过训练好的逻辑回归模型，预测平面上这些点的分类
	y_predict = model.predict(X_grid_matrix)
	y_predict_matrix = y_predict.reshape(X0.shape)
	
	# 设置色彩表
	from matplotlib.colors import ListedColormap
	my_colormap = ListedColormap(['#0000CD', '#40E0D0', '#FFFF00'])
	
	# 绘制等高线，并且填充等高区域的颜色
	plt.contourf(X0, X1, y_predict_matrix, linewidth=5, cmap=my_colormap)

plot_decision_boundary(rbf_svc, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y==0, 0], X[y==0, 1])
plt.scatter(X[y==1, 0], X[y==1, 1])
plt.show()

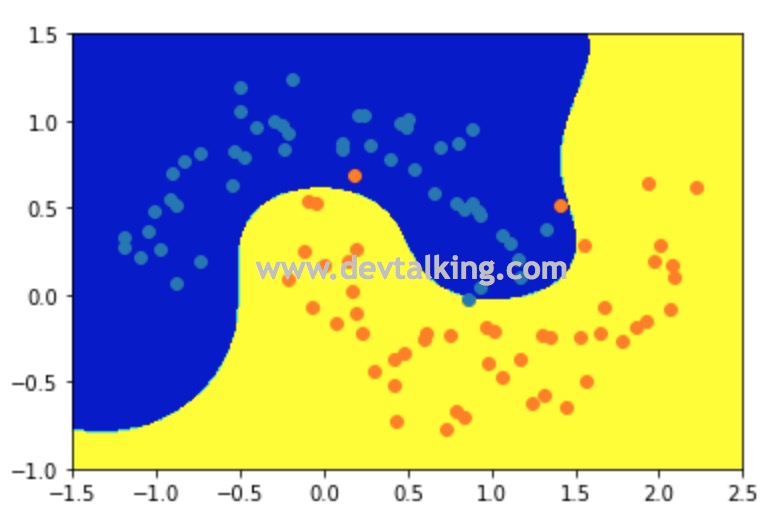
上图就是当$\gamma$为1时，RBF SVM训练样本数据后的决策边界，我们先来解释一下它的高斯分布有什么关系。

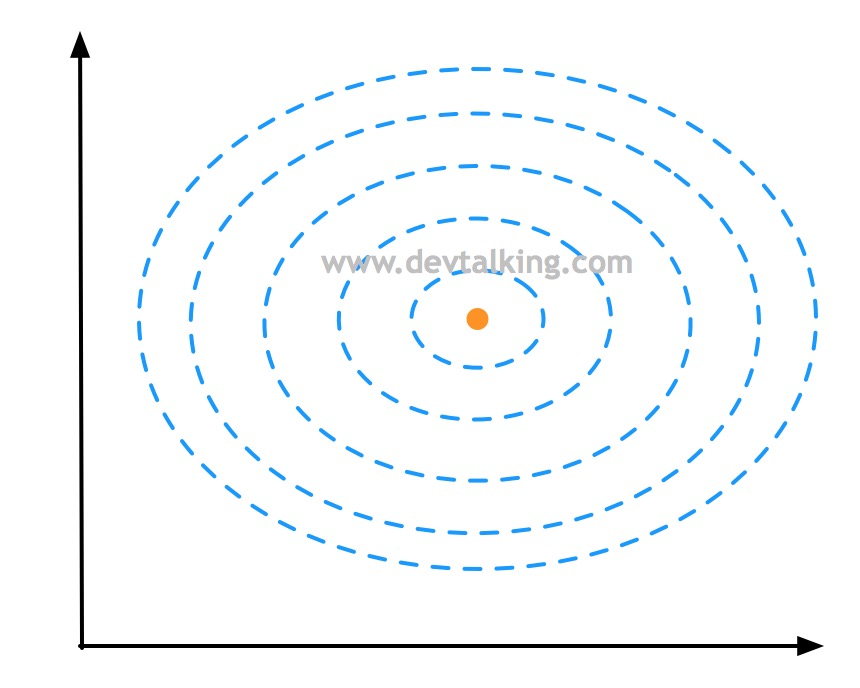
如上图所示，蓝色虚线表示等高线，橘黄色点表示一个样本点，所以上面的图其实是俯视以橘黄色样本点为峰值点的高斯分布图。

对于每个样本点都有围绕它的一个高斯分布图，所以连起来就形成了一片区域，然后形成了决策区域和决策边界：

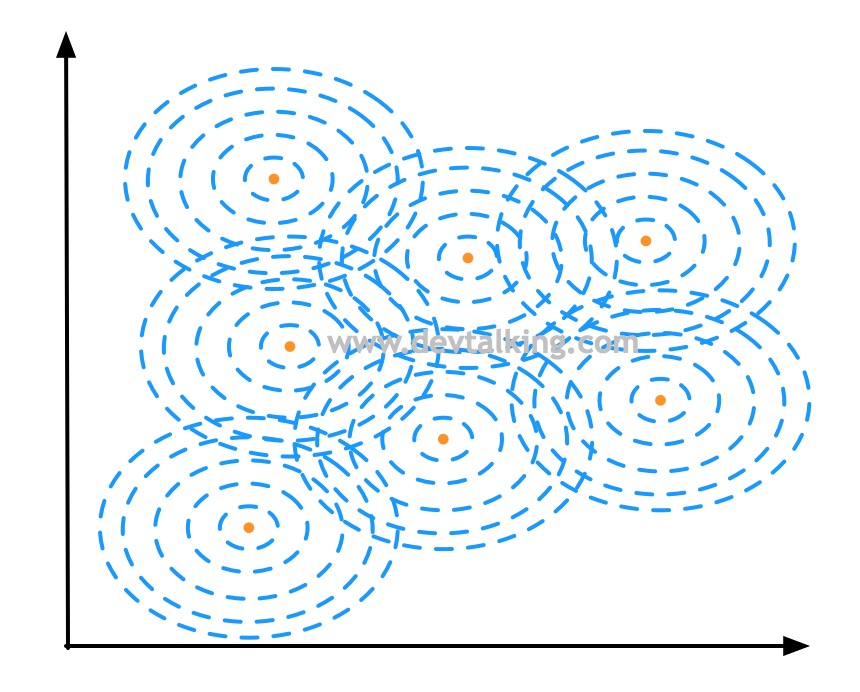
可以看到当$\gamma$取1时，RBF SVM训练样本数据后的决策边界和多项式SVM的几乎一致。下面我们尝试变化超参数$\gamma$来看看决策边界会有怎样的变化。

先来看看将$\gamma$取较大值后的决策边界：

# 将gamma取100
rbf_svc100 = RBFKernelSVC(gamma=100)
rbf_svc100.fit(X, y)

plot_decision_boundary(rbf_svc100, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y==0, 0], X[y==0, 1])
plt.scatter(X[y==1, 0], X[y==1, 1])
plt.show()

从上图可以看到，决策边界几乎就是围绕着蓝色点的区域，这也印证了高斯核函数中$\gamma$越大、高斯分布峰值越大，既钟形越窄的定义。因为钟形比较窄，所以不足以连成大片区域，就呈现出了上图中的情况。

我们再来看看将$\gamma$取较小值后的决策边界：

rbf_svc01 = RBFKernelSVC(gamma=0.1)
rbf_svc01.fit(X, y)

plot_decision_boundary(rbf_svc01, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y==0, 0], X[y==0, 1])
plt.scatter(X[y==1, 0], X[y==1, 1])
plt.show()

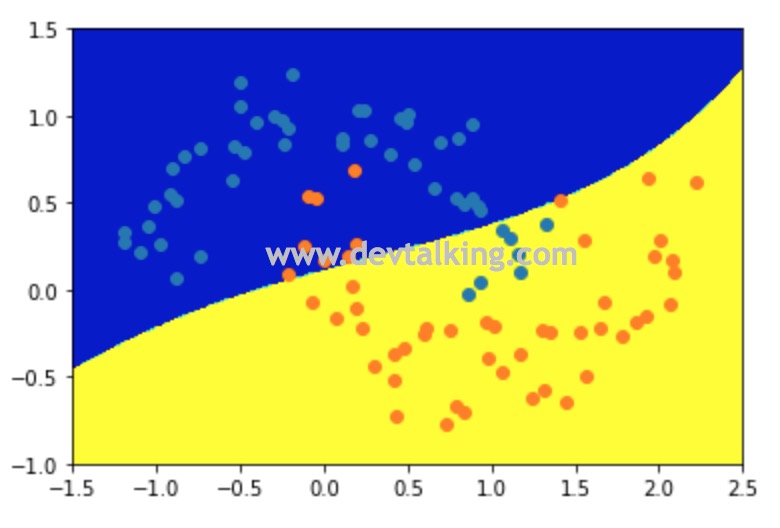
可以看到当$\gamma$取0.1后，决策边界几乎成了线性决策边界，说明每个样本点的高斯分布钟形太宽了。所以我们得出结论，当$\gamma$取值比较大时，数据训练结果趋于过拟合，当$\gamma$取值比较小时，数据训练结果趋于欠拟合。

SVM解决回归问题

SVM解决回归问题的思路和解决分类问题的思路正好是相反的。我们回忆一下，在Hard Margin SVM中，我们希望在Margin区域中一个样本点都没有，即便在Soft Margin SVM中也是希望Margin区域中的样本点越少越好。

而在SVM解决回归问题时，是希望Margin区域中的点越多越好：

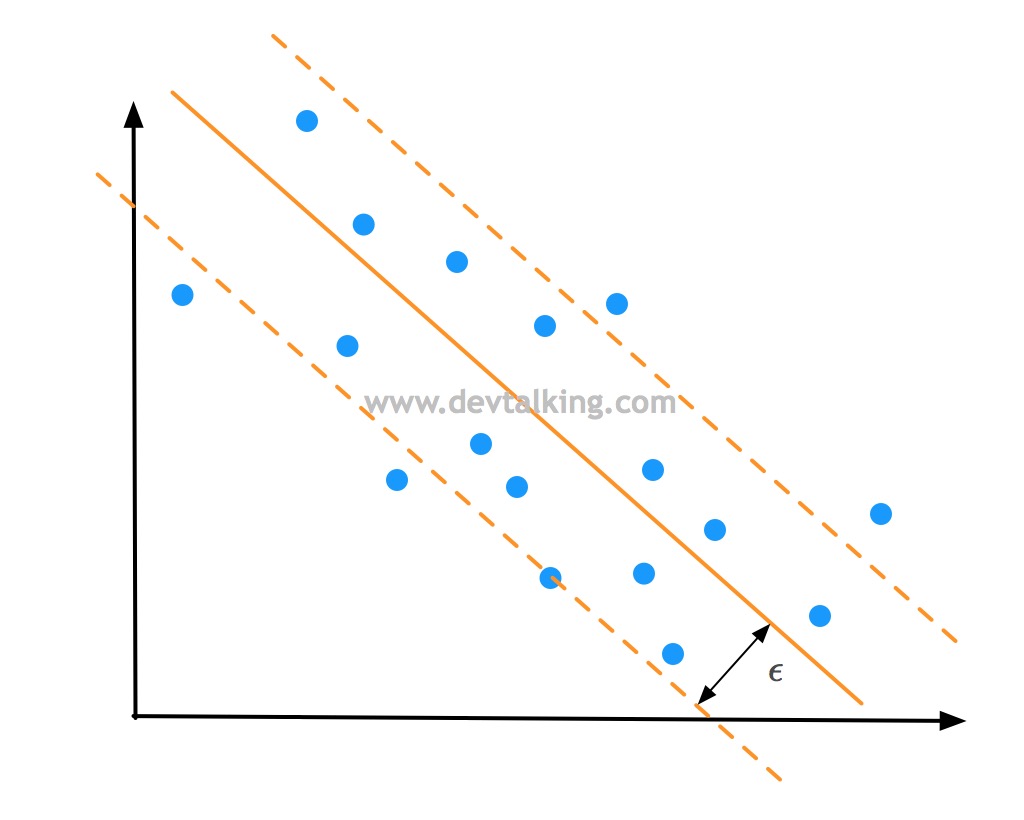
也就是找到一条拟合直线，使得这条直线的Margin区域中的样本点越多，说明拟合的越好，反之依然。Margin边界到拟合直线的距离称为$\epsilon$是SVM解决回归问题的一个超参数。

在Scikit Learn中有LinearSVR和SVR两个类，前者就是使用SVM线性方式解决回归问题的类，后者是SVM使用核函数方式解决回归问题的类。用法和LinearSVC及SVC的一致，只不过需要传入$\epsilon$这个超参数既可。

申明：本文为慕课网liuyubobobo老师《Python3入门机器学习 经典算法与应用》课程的学习笔记，未经允许不得转载。