这一篇笔记主要讲机器学习算法中一个重要的分类算法,支撑向量机(Support Vector Machine)。它背后有严格的数学理论和统计学理论支撑的,这里我们只对它的原理和应用做以介绍,更深层次的数学理论有兴趣可以查阅其他资料。
什么是SVM

上面的图展示的是一个二分类问题,在逻辑回归的笔记中,我们知道了决策边界,图中橘黄色的直线就是决策边界,它看似很好的将样本数据的不同分类区分开了。我们在多项式回归的笔记中,讲过模型泛化的问题,一个模型的好坏程度很大程度上是体现了模型泛化能力的好坏,也就是对未知样本的预测能力。
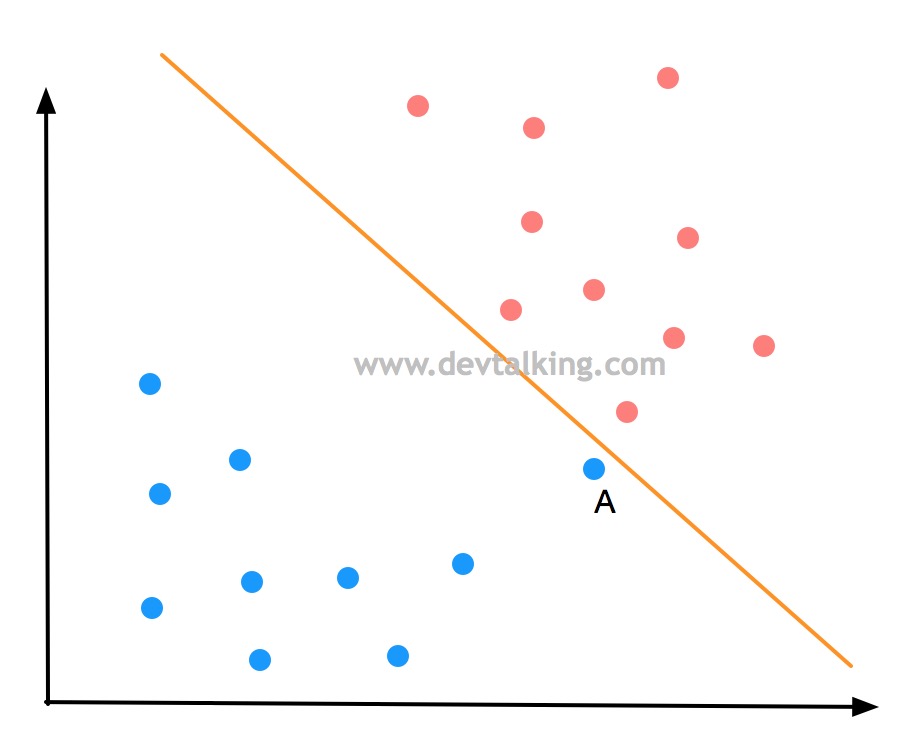
如果新来一个样本数据A,按照决策边界划分它是被分为了蓝色分类,可事实真的是如此吗,因为点A和红色分类的点非常近,很有可能点A是属于红色分类的。所以上图中的决策边界可能并不是最优的,那最优的决策边界应该是什么样的呢?
上面的决策边界之所以有缺陷,是因为它和红色类别的点太近了,当然肯定也不能和蓝色的点太近了,所以我们希望这条决策边界离红色分类和蓝色分类都尽可能的远,才能很好的避免上面出现的问题。
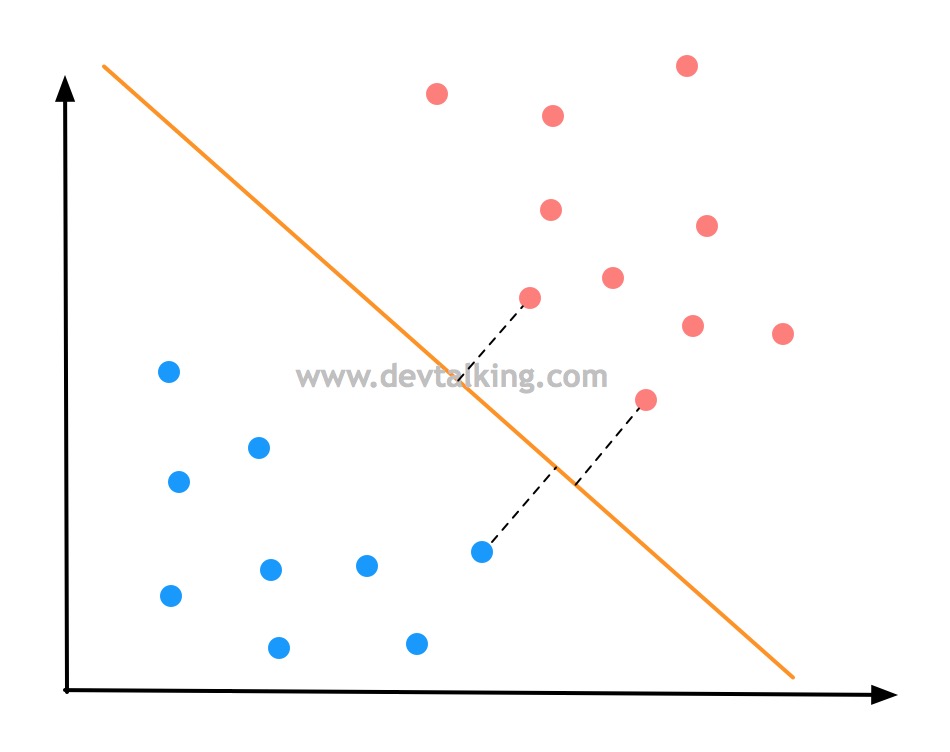
想要决策边界离红蓝两个分类都尽可能的远,也就是红蓝分类两边离决策边界最近的点的距离要远,并且两边的点到决策边界的距离要相等,这才说明决策边界是不偏不倚的,如上图所示。
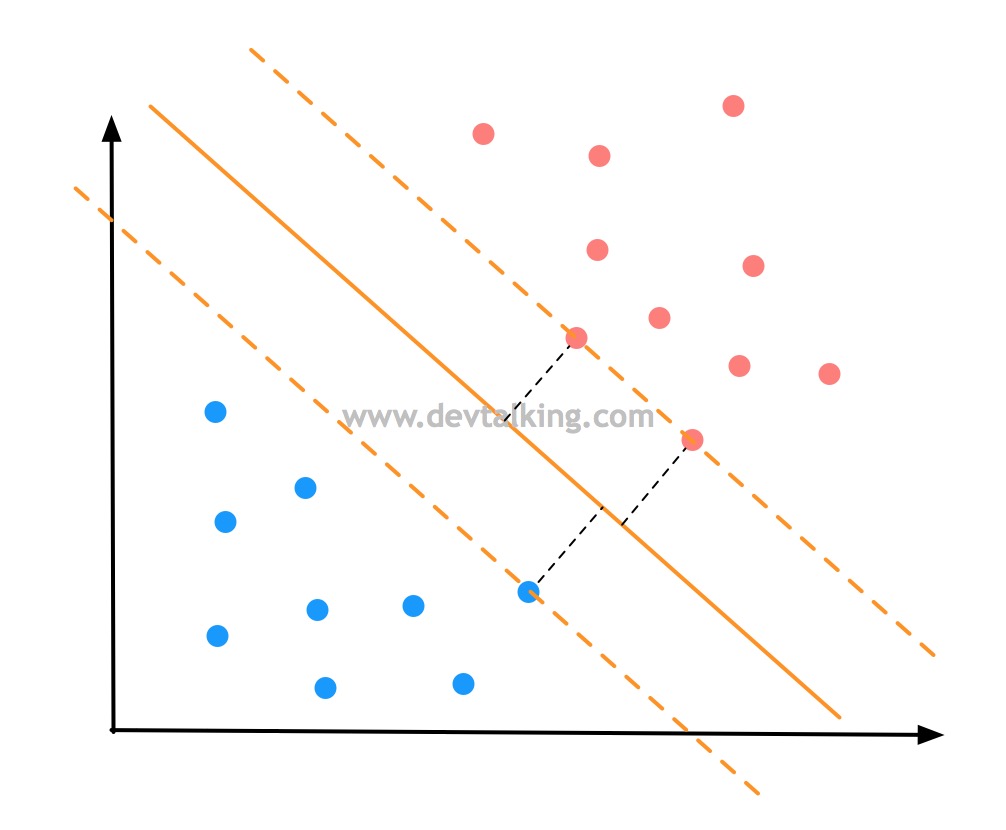
过红蓝两边离决策边界最近的点画两条直线,并且平行于决策边界,那么就确定了一个区域,在这个区域内不应该再有任何数据点出现。那么SVM就是尝试寻找这个区域中间那条最优的决策边界。这个区域边界上的点称为支撑向量,换句话说,是支撑向量定义出了这个区域,那么最优的决策边界也是由支撑向量决定的,这也是支撑向量机这个名称的由来。
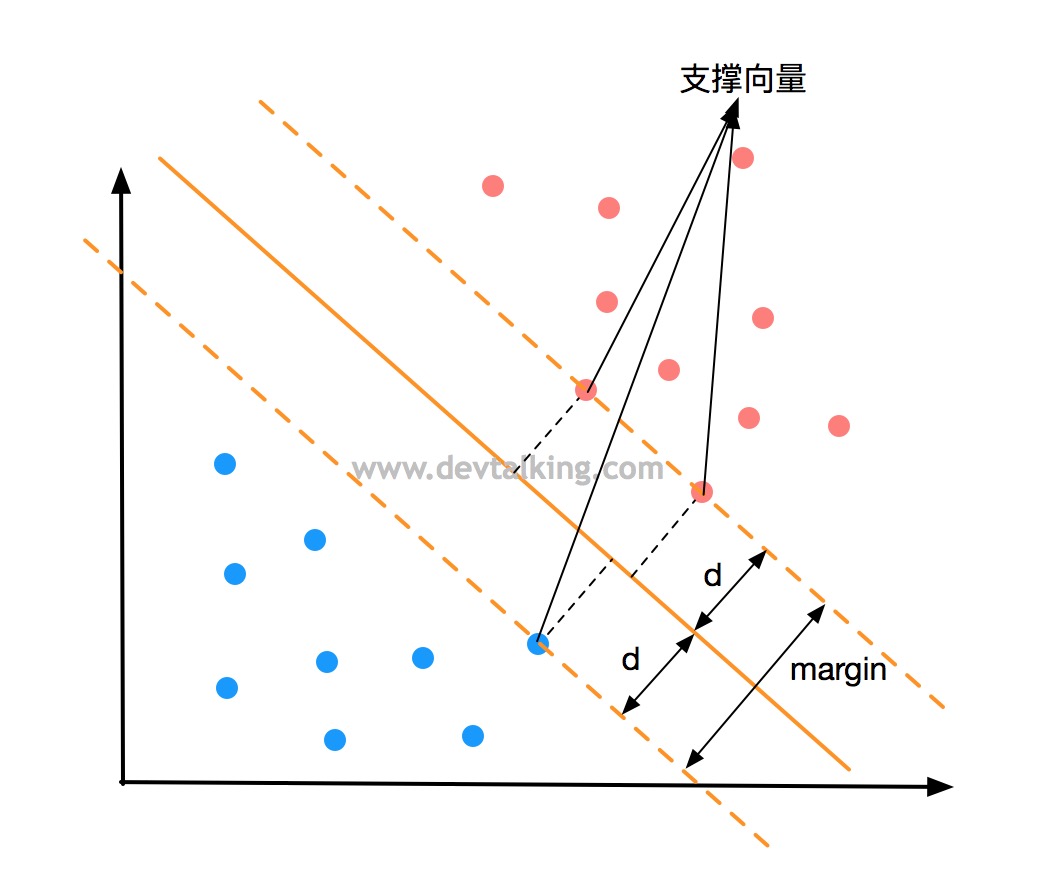
如上图所示,由支撑向量确定的区域之间的距离称为Margin。那么SVM要做的事情就是最大化Margin,既将问题转化为了求最优解的问题。
以上对SVM的解释是基于线性可分问题的基础上,也就是能确确实实找到一条直线作为决策边界,这种问题称为Hard Margin SVM,但是很多真实的情况是线性不可分的,这类问题称为Soft Margin SVM,这两类问题都是支撑向量机可以处理的,但基础还是Hard Margin SVM。
SVM背后的最优化问题
从上面的示例图上可以看出,Margin其实就是二倍的$d$,$d$是支撑向量到决策边界的距离,那么求Margin的最大值就是求$d$的最大值。
点到直线的距离
在解析几何中我们学过,假设有条直线定义为$ax + by + c = 0$,有一点的坐标为$(x_0, y_0)$,那么该点到该条直线的距离为:
$$d = \frac {|ax_0 + by_0 + c|} {\sqrt{a^2 + b^2}}$$
那么如果扩展到高维空间中,点到直线的距离为:
$$d = \frac {|ax_0 + by_0 + cz_0 + d|} {\sqrt{a^2 + b^2 + c^2}}$$
上面公式中的$x_0$、$y_0$、$z_0$可以看作样本数据的特征,而$a$、$b$、$c$可以看作是特征系数。那么上面的公式可以写为:
$$d = \frac {|ax_1 + bx_2 + cx_3 + d|} {\sqrt{a^2 + b^2 + c^2}}$$
将$ax_1 + bx_2 + cx_3$向量化后,公式可写为:
$$d = \frac {|w^Tx + d|} {\sqrt{a^2 + b^2 + c^2}}$$
再根据向量的模的公式$||\vec v|| = \sqrt {v_1^2 + v_2^2 + … + v_n^2}$,上面的公式可继续转换为:
$$d = \frac {|w^Tx + d|} {||w||}$$
$w$为特征系数向量,$x$为特征向量。
限定条件的最优化问题
有了上面的公式后,我们就可以假定决策边界直线的公式为$w^Tx + d = 0$,支撑向量到它的距离为$d = \frac {|w^Tx + d|} {||w||}$。那么除了支撑向量以外的点到决策边界的距离都应该大于$\frac {|w^Tx + d|} {||w||}$。
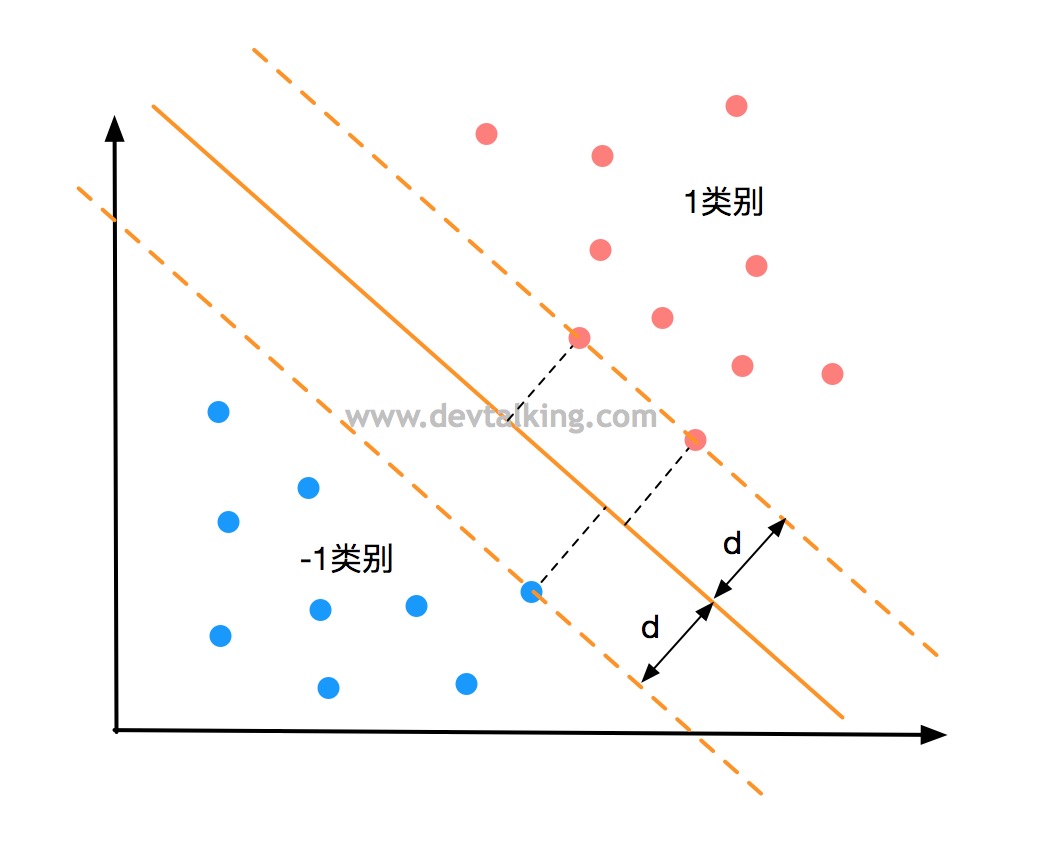
我们将上图中红色点定义为1类别,蓝色点定义为-1类别,那么就有:
$$\left\{
\begin{aligned}
{\frac {w^Tx^{(i)} + d} {||w||} \ge d \ \ \ \ \ \ \forall y^{(i)} = 1 \\
\frac {w^Tx^{(i)} + d} {||w||} \le -d \ \ \ \ \ \ \forall y^{(i)} = -1}
\end{aligned}
\right.
$$
既任意类别为1的红色点距离决策边界的距离要大于等于$d$。任意类别为-1的蓝色点距离决策边界的距离要小于等于$-d$。将上面的两个公式左右分别除以$d$得:
$$\left\{
\begin{aligned}
{\frac {w^Tx^{(i)} + d} {||w||d} \ge 1 \ \ \ \ \ \ \forall y^{(i)} = 1 \\
\frac {w^Tx^{(i)} + d} {||w||d} \le -1 \ \ \ \ \ \ \forall y^{(i)} = -1}
\end{aligned}
\right.
$$
下面来分析上面的公式,$||w||$是一个标量,$d$也是一个标量,所以分母$||w||d $也是一个标量。那么对于分子中的向量$w^T$除以一个标量仍然是一个向量,可以记为$w^T_d$。分子中的标量$d$除以一个标量自然也是一个标量,记为$d_d$。所以上面的公式又可以转换为:
$$\left\{
\begin{aligned}
{w^T_dx^{(i)} + d_d \ge 1 \ \ \ \ \ \ \forall y^{(i)} = 1 \\
w^T_dx^{(i)} + d_d \le -1 \ \ \ \ \ \ \forall y^{(i)} = -1}
\end{aligned}
\right.
$$
这样也就得出了由红色点支撑向量构成的直线公式为:
$$w^Tx + d = 1$$
由蓝色点支撑向量构成的直线公式为:
$$w^Tx + d = -1$$
在逻辑回归的笔记中我们知道通过一个技巧可以将上面两个公式通过一个公式表示出来,既公式左右两边都乘以$y^{(i)} $,得:
$$y^{(i)}(w^T_d x^{(i)} + d_d) \ge 1$$
为了书写方便,我们就将$w^T_d $和$d_d$命名为$w^T$和$d$。所以最终我们希望的是对于所有的样本数据点都满足下面的公式:
$$y^{(i)}(w^T x^{(i)} + d) \ge 1$$
那么上面这个公式就是SVM中最优化目标函数的限定条件,标识为$S.T.$(Such That)。
目标函数
在这一节开始时我们就很明确我们的目标是求$d$的最大值,既:
$$max \frac {|w^Tx + d|} {||w||}$$
根据之前的推导我们知道,无论是红色点的支撑向量,还是蓝色点的支撑向量构成的直线公式取绝对值后都为1,所以我们的目标函数又可以写为:
$$max \frac 1 {||w||}$$
既:
$$min ||w||$$
为了方便求导,我们再将其转换一下,最终SVM的目标函数为:
$$min \frac 1 2 ||w||^2$$
那么最后SVM的最优化问题的两个函数为:
$$\left\{
\begin{aligned}
{min \frac 1 2 ||w||^2 \\
S.T. \ \ \ y^{(i)}(w^T x^{(i)} + d) \ge 1}
\end{aligned}
\right.
$$
也就是在$y^{(i)}(w^T x^{(i)} + d) \ge 1$这个限定条件下 ,求目标函数$min \frac 1 2 ||w||^2 $的最优解。
这就和我们之前学习过的算法不一样了,之前不论是线性回归还是逻辑回归,在求最优化问题时都是求全局最优化问题,也就是没有限定条件的目标函数最优解问题,这类问题对目标函数求导让他等于0,然后相应的极值点就是最大值或最小值的位置。而SVM是有条件的最优化问题,此时求目标函数的极值就复杂了很多,这里就不对求解过程做详细阐述了。
Soft Margin SVM
在上一节介绍了Hard Margin SVM和Soft Margin SVM,并且在诠释SVM背后最优化问题的数学原理时也是基于Hard Margin SVM前提的。这一节我们来看看Soft Margin SVM。
Soft Margin SVM概念
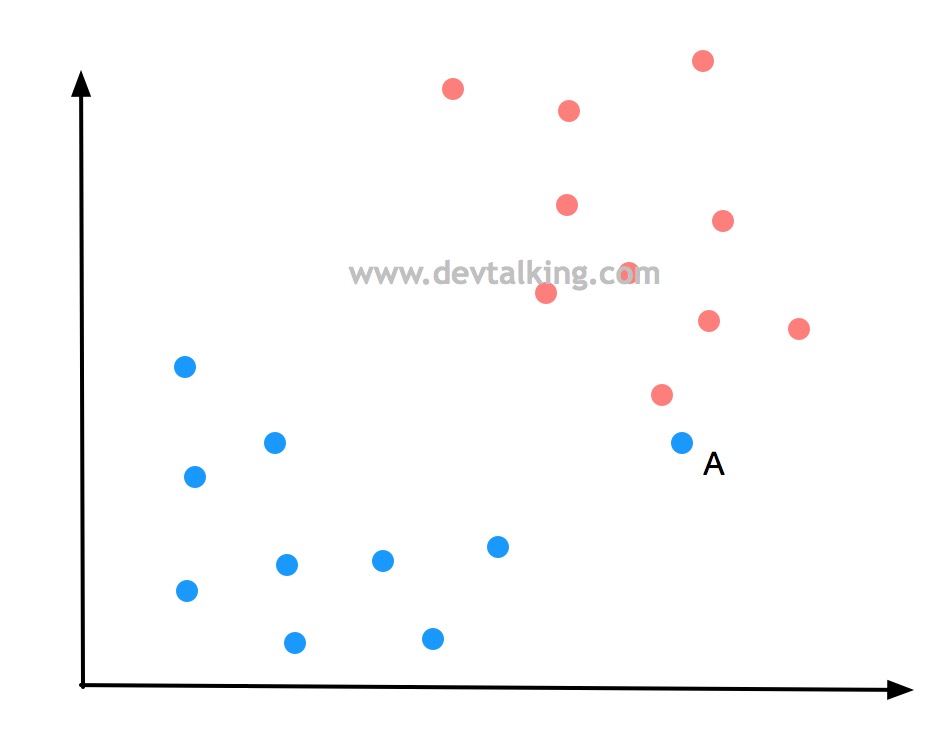
如上图所示,点A是一个蓝色分类的点,但是它离红色分类的点非常近,那么如果按Hard Margin SVM的思路,上图情况的决策边界很有可能是下图所示这样:
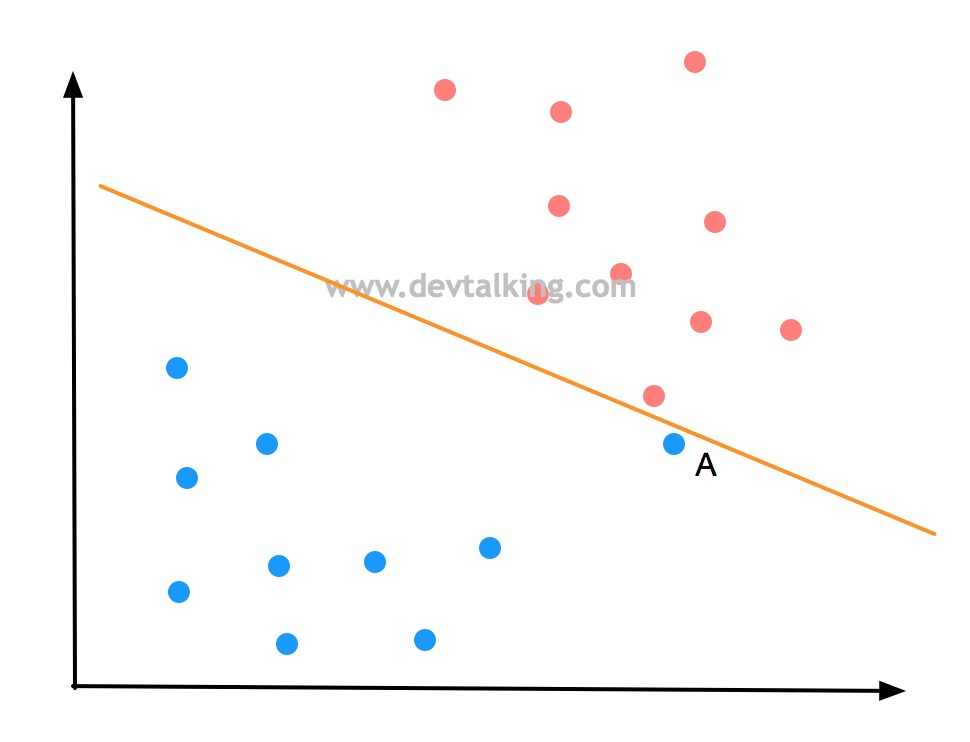
这条决策边界直线看似很好的将蓝色和红色点完全区分开了,但是它的泛化能力是值得怀疑的,因为这条决策边界极大的受到了点A的影响,而点A可能是蓝色点中极为特殊的一个点,也有可能它根本就是一个错误的点。所以根据SVM的思想,比较合理的决策边界应该下图绿色的直线所示:

虽然绿色直线的决策边界没有完全将红蓝点分开,但是如果将它放在生产数据中,可能预测准确度更高,也就是泛化能力更强。
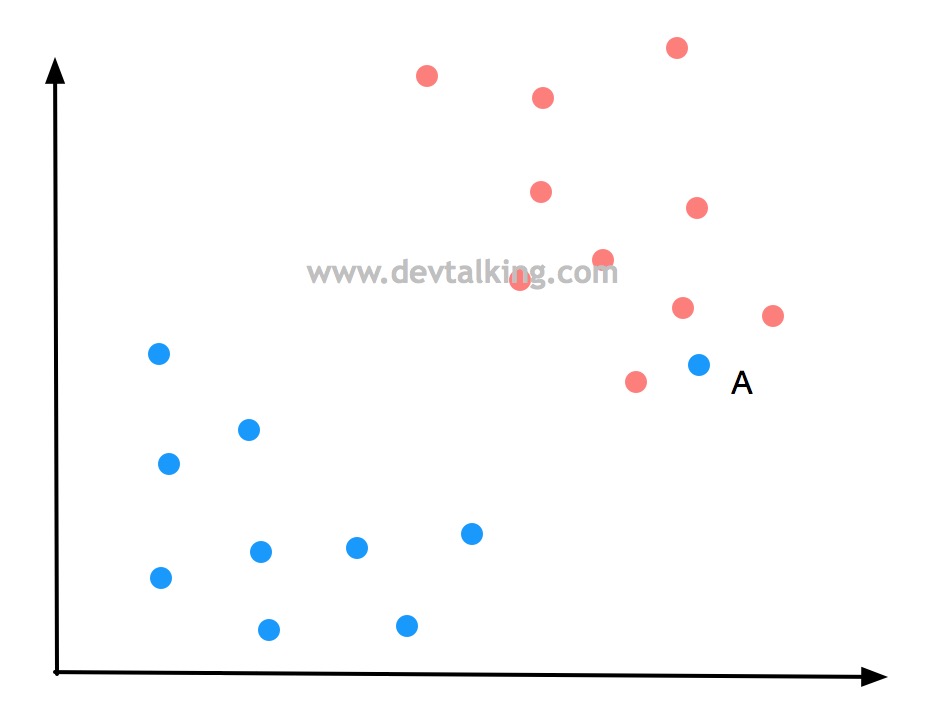
再如上图中的情况,已经根本不可能有一条线性决策边界能将红蓝点分开了,所以我们希望决策边界具有一定的包容性或容错性,已降低分类准确度的代价换来更高的泛化能力。那么这种SVM就称为Soft Margin SVM。
Soft Margin SVM原理
在Hard Margin SVM最优化问题的两个函数中,限定条件$y^{(i)}(w^T x^{(i)} + d) \ge 1$表示在Margin区域内不会有任何点出现,但是在Soft Margin SVM中为了容错性,是允许在Margin区域内出现点的,也就是将Hard Margin SVM的限定条件加以宽松量,并且这个宽松量必须是正数:
$$S.T. \ \ \ y^{(i)}(w^T x^{(i)} + d) \ge 1 - \zeta_i$$
$$\zeta_i \ge 0$$

上图中有四条直线,其中橘黄色的三条是在讲Hard Margin SVM中得出的,如果我们将Hard Margin SVM中的限定条件加以宽松量的话,其实Margin的区域就会变小,也就是图中绿色虚线和决策边界构成的区域。而绿色虚线的方程为:
$$w^Tx + d = 1 - \zeta$$
那么Soft Margin SVM的限定条件我们就知道了。
但是现在问题来了,如果当$\zeta$无穷大时会发生什么情况呢?那就意味着容错性无穷大,也就是可以将所有点都认为是同一类了,故而分不出类别。解决这个问题的思路我们之前已经了解过了,那就是模型正则化。
我们知道Hard Margin SVM的优化目标函数为$min \frac 1 2 ||w||^2$,Soft Margin SVM也是基于Hard Margin SVM的思想演变的,所以我们将这个目标函数加一个正则模型,而这个正则模型又恰是Soft Margin SVM的宽松量,这样就达到了在Hard Margin SVM的思路下,增加宽松量从而实现Soft Margin SVM,所以 Soft Margin SVM的目标函数为:
$$min \frac 1 2 ||w||^2 + C \sum_{i=1}^m\zeta_i$$
公式里的$C$是模型正则化中的一个超参数,取值范围在0到1之间。用来权衡Hard Margin SVM目标函数和Soft Margin SVM宽松量两者之间的比例。如此一来也就限制了$\zeta$无穷大的问题,因为Soft Margin SVM的目标函数最优化要同时估计两部分,相互制约。
我们在之前的笔记中学习过了$L_p$范数及$L_p$正则模型。这里的$C \sum_{i=1}^m\zeta_i$就是$L_1$正则模型,而$L_2$正则模型是$C \sum_{i=1}^m\zeta_i^2$。
模型正则化的内容请参见 机器学习笔记九之交叉验证、模型正则化 。
Scikit Learn中的SVM
前面两小节介绍了SVM背后的数学原理,这一节来看看如何使用Scikit Learn中封装的SVM方法。我们还是使用之前使用过很多次的鸢尾花数据:
import numpy as np |
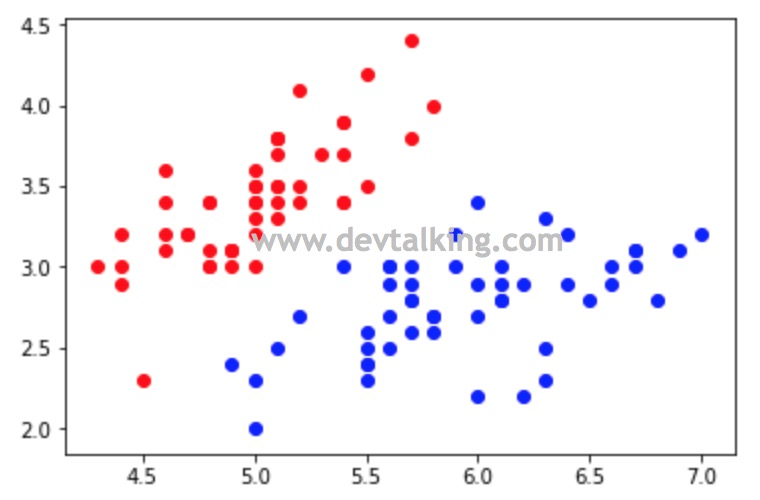
接下来我们使用Scikit Learn封装的SVM方法对样本数据进行分类:
from sklearn.svm import LinearSVC |

在上面的示例代码中,我将超参数$C$取了一个非常大的数,那么为了平衡$min \frac 1 2 ||w||^2 + C \sum_{i=1}^m\zeta_i$整个函数,$\zeta$就得等于0才能让最大限度的平衡正则模型和整个目标函数。所以宽松量为零,就成了Hard Margin SVM。并且从上图可以看出,离决策边界最近的点,无论是红色点还是蓝色点,也就是红蓝支撑向量到决策边界的距离都差不多。
如果我们将超参数$C$的值取的小一些,那么整个问题就变成了Soft Margin SVM,来对比看看决策边界会有什么不同:
svc2 = LinearSVC(C=0.01) |

此时从上图可以看到,红蓝支撑向量到决策边界的距离已经不一样了,并且还有一个红色的点被划到蓝色点的范围内,那么我们知道这都是因为Soft Margin SVM中加了宽松量的缘故。
绘制支撑向量直线
在上一小节,我们知道决策边界以及上下支撑向量构成的直线的公式分别是:
- 决策边界:$w^Tx + d = 0$
- 上支撑向量直线:$w^Tx + d = 1$
- 下支撑向量直线:$w^Tx + d = -1$
那么在鸢尾花的示例中,如何来求这三条直线呢?以决策边界直线为例,$w$和$d$其实我们已经知道了,就是特征系数和截距:
svc.coef_ |
因为我们只用了鸢尾花的两个类型和两个特征,所以决策边界直线的公式可以展开为:
$$w_0 * x_0 + w_1 * x_1 + d = 0$$
将上面的公式转换为$y = ax + b$的形式:
$$w_1 * x_1 = - w_0 * x_0 - d \\
x_1 = - \frac {w_0 * x_0} {w_1} - \frac {d} {w_1}$$
同理我们也可以将支撑向量直线的公式作以转换:
$$x_1 = - \frac {w_0 * x_0} {w_1} - \frac {d} {w_1} + \frac 1 {w_1}$$
$$x_1 = - \frac {w_0 * x_0} {w_1} - \frac {d} {w_1} - \frac 1 {w_1}$$
此时我们在给定的坐标系内,构建一组$x_0$,那么就可以求出一组$x_1$,然后将这些点连起来,就绘制出了决策边界的直线:
# 构造一个绘制决策边界和上下支撑向量直线的方法 |
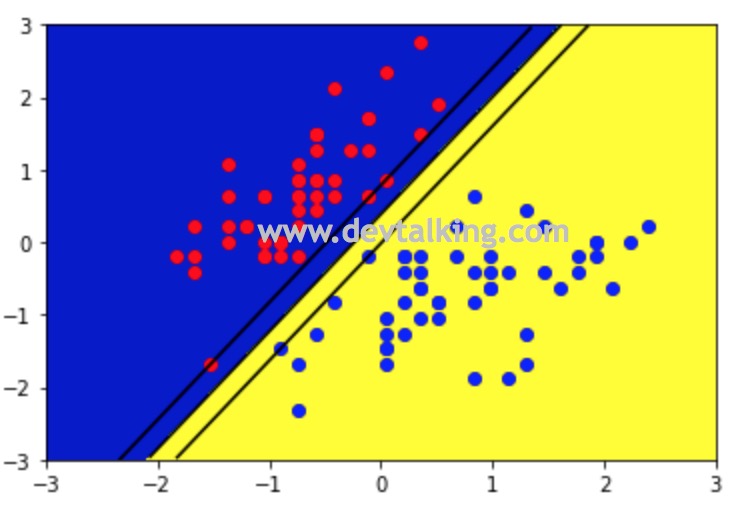
从上图可以看到,是一个标准的Hard Margin SVM,Margin区域没有任何一个点,支撑向量一共有五个,红色点三个,蓝色点两个。
我们再来看看Soft Margin SVM的情况:
plot_decision_boundary(svc2, axis=[-3, 3, -3, 3]) |
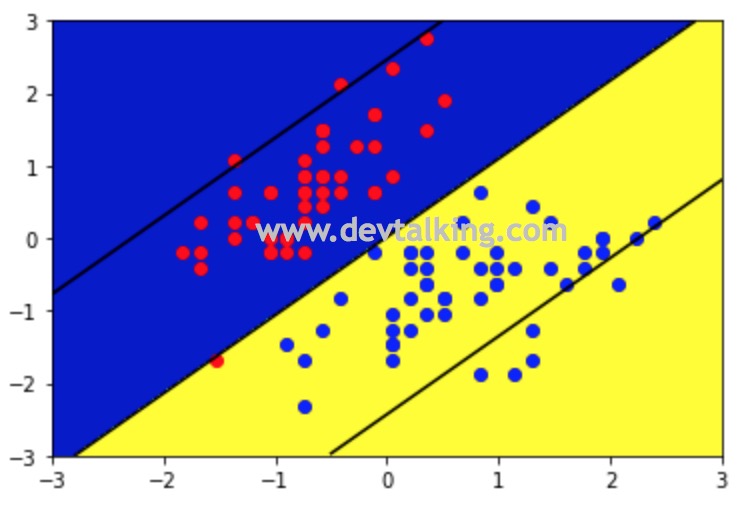
从上图中可以看出,Margin区域内有很多点,说明相比Hard Margin SVM,Soft Margin SVM增加了不少宽松量。
申明:本文为慕课网liuyubobobo老师《Python3入门机器学习 经典算法与应用》课程的学习笔记,未经允许不得转载。