这篇笔记我们来看看机器学习中一个重要的非参数学习算法,决策树。
什么是决策树
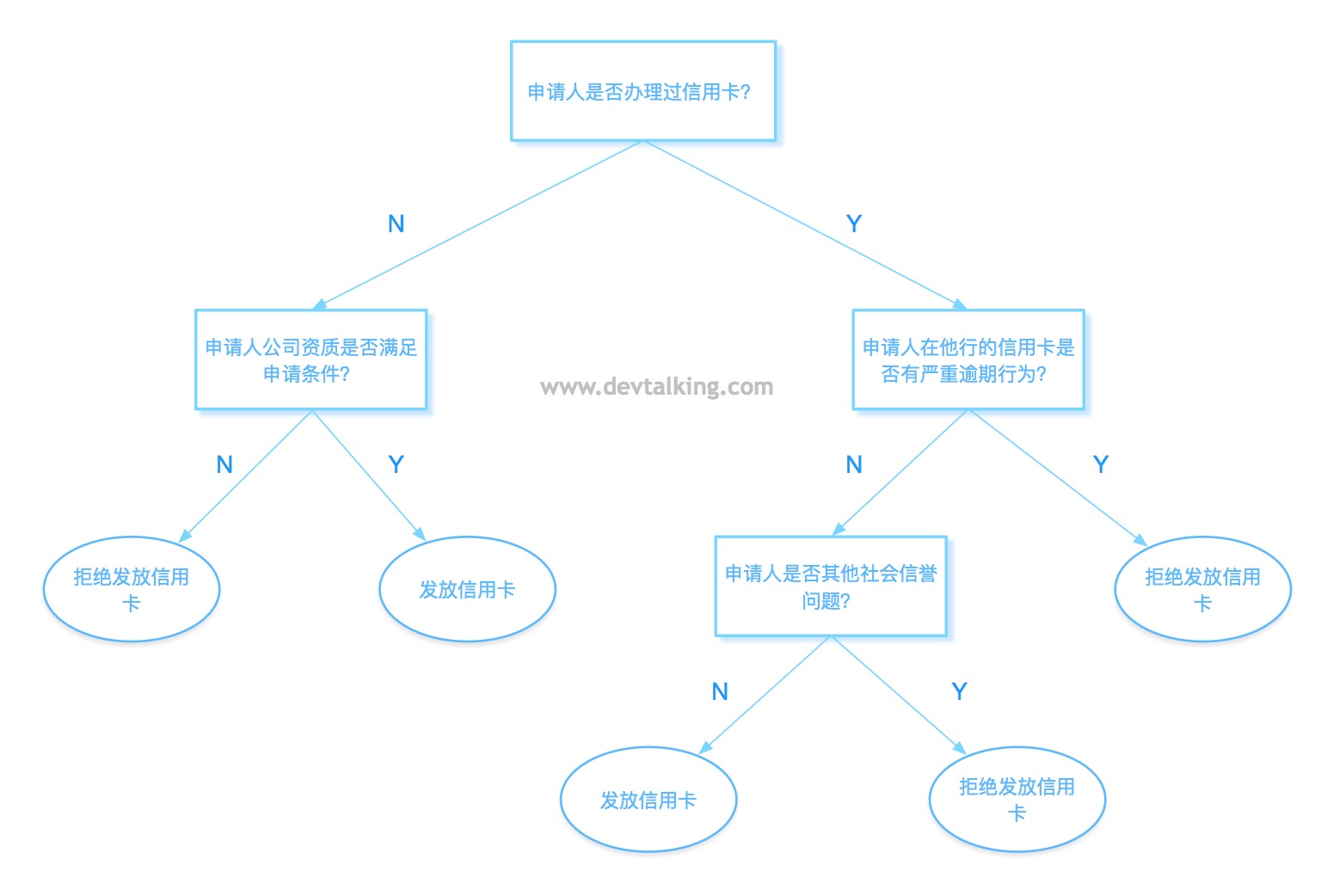
上图是一个向银行申请信用卡的示例,图中的树状图展示了申请人需要在银行过几道关卡后才能成功申请到一张信用卡的流程图。在图中树状图的根节点是申请人输入的信息,叶子节点是银行作出的决策,也就相当于是对申请者输入信息作出的分类决策。从第一个根节点到最后一个叶子节点经过的根节点数量称为树状图的深度(depth)。上图示例中的树状图从第一个根节点申请人是否办理过信用卡,到最后一个发放信用卡叶子节点共经过了三个根节点,所以深度为3。那么像这样使用树状图对输入信息一步步分类的方式就称为决策树方式。
我们再来看一个问题,上图中每一个根节点的输入信息都可以用是或否来做判断分类,但是机器学习的样本数据都是数字,那么此时如果做判断呢?我们先来使用Scikit Learn中提供的决策树直观的看一下通过决策树对样本数据的分类过程和分类结果。
# 我们使用Scikit Learn提供的鸢尾花数据集 |
# 引入Scikit Learn中的决策树分类器 |
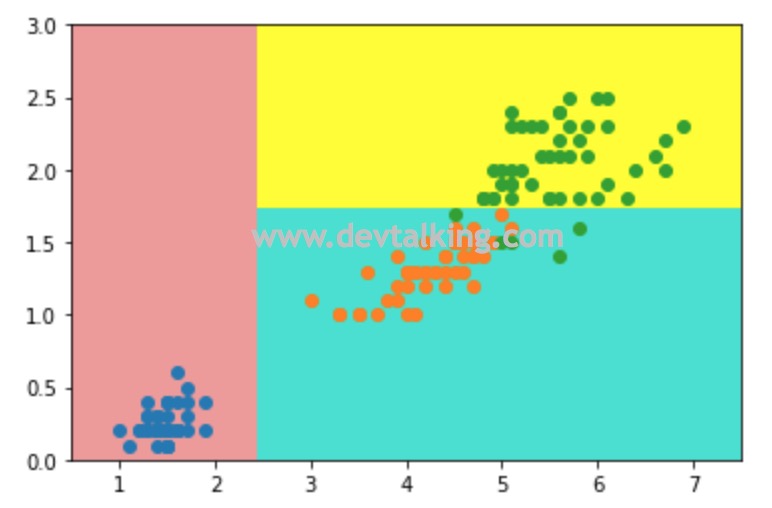
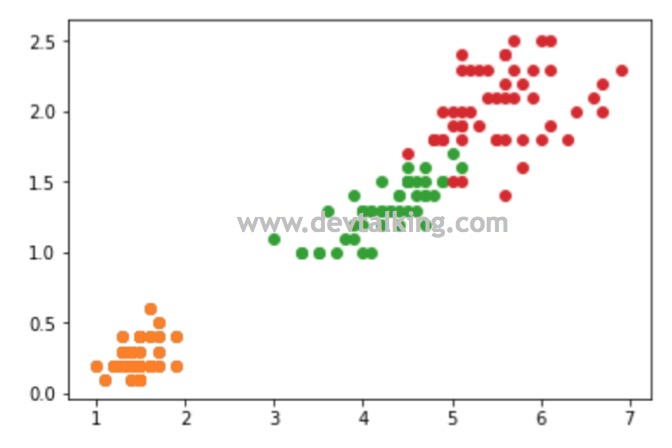
从决策边界图中可以看到决策树分类器将鸢尾花的数据较好的进行的归类区分。那么再回到刚才的问题,那就是在对样本数据进行决策树分类时,根节点是怎么做判断的呢?
我们仔细看上图,假设我们将横轴表示的特征记为$x$,纵轴表示的特征记为$y$,那么红色的区域就是$x<2.4$的区域,所以第一个根节点就直接可定义为$x$是否小于2.4,既样本数据的某一个特征数值是否小于2.4,如果小于2.4,那么将该样本点判定为蓝色分类的点。
然后再来看纵轴,观察可得,$y=1.8$是蓝色和黄色区域的分界点,所以可将$y<1.8$作为第二层的根节点,如果样本数据的另一个特征数值小于1.8,则判定为黄色分类的点,大于1.8则判定为绿色分类的点。那么此时的决策树为:

也就是决策树在对样本数据分类时,会先选定一个维度,或者说一个特征,再选定和这个维度想对应阈值构成一个根节点,既判断条件。
通过上面的示例,大家应该什么是决策树有了直观的了解,并且也能看出来决策树的一些特点:
- 决策树算法是非参数学习算法。
- 决策树算法可以解决分类问题。
- 决策树算法可以天然解决多分类问题。
- 决策树算法处理样本数据的结果具有非常好的可解释性。
了解了决策树后,那么问题来了,对于决策树来说核心的工作是确定根节点,那么这个根节点该如何确定呢?在哪个维度做划分?某个维度在哪个值上做划分?我们往后看。
信息熵
这一节我们先来看看什么是信息熵。其实信息熵的概念很简单,熵在信息论中代表随机变量不确定的度量。
- 熵越大,数据的不确定性越高。
- 熵越小,数据的不确定性越低。
信息熵的公式
上面解释了信息熵的定义,那么这一小节我们使用信息熵的公式来解释它的定义。
$$H = - \sum_{i=1}^k p_i log(p_i)$$
上面的公式就是香农提出的信息熵的公式。逐个解释一下:
- 假如一组数据有k类信息,那么每一个信息所占的比例就是$p_i$。比如鸢尾花数据包含三种鸢尾花的数据,那么每种鸢尾花所占的比例就是$\frac 1 3$,那么$p_1$、$p_2$、$p_3$就分别为$\frac 1 3$。
- 因为$p_i$只可能是小于1的,所以$log(p_i)$始终是负数。所以需要在公式最前面加负号,让整个熵的值大于0。
我们来举几个例子看一下,首先用鸢尾花的例子,三种鸢尾花各占$\frac 1 3$:
$$\{\frac 1 3,\frac 1 3,\frac 1 3\}$$
那么代入信息熵的公式可得:
$$H=-\frac 1 3 log(\frac 1 3)-\frac 1 3log(\frac 1 3)-\frac 1 3log(\frac 1 3)=1.0986$$
再来看一个例子:
$$\{\frac 1 {10},\frac 2 {10},\frac 7 {10}\}$$
代入公式可得:
$$H=-\frac 1 {10} log(\frac 1 {10})-\frac 2 {10}log(\frac 2 {10})-\frac 7 {10}log(\frac 7 {10})=0.8018$$
从上面两个例子可以看出,第二个例子的信息熵比一个例子的小,那么意味着第二个示例的数据不确定性要低于第一个示例的数据。其实从数据中也能看出,其中有一类信息占全部信息的$\frac 7 {10}$,所以大多数据是能确定在某一类中的,故而不确定性低。而第一个示例中每类信息都占了全部信息的$\frac 1 3$,所以数据不能很明确的确定是哪类,故而不确定性高。
再来看一个极端的例子,$\{1,0,0\}$,将其代入信息熵公式后得到的值是0。因为整个数据中就一种类型的数据,所以不确定性达到了最低,既信息熵的最小值为0。
信息熵曲线
这一小节我们在Jupyter Notebook中将信息熵的曲线绘制出来再让大家感性的理解一下。假设一组信息中有两个类别,那么当一个类别所占比例为$x$时,另一个类别的所占比例肯定是$1-x$,将其代入信息熵的公式展开后可得:
$$H=-xlog(x)-(1-x)log(1-x)$$
下面我们用代码来绘制一下这个曲线:
import numpy as np |
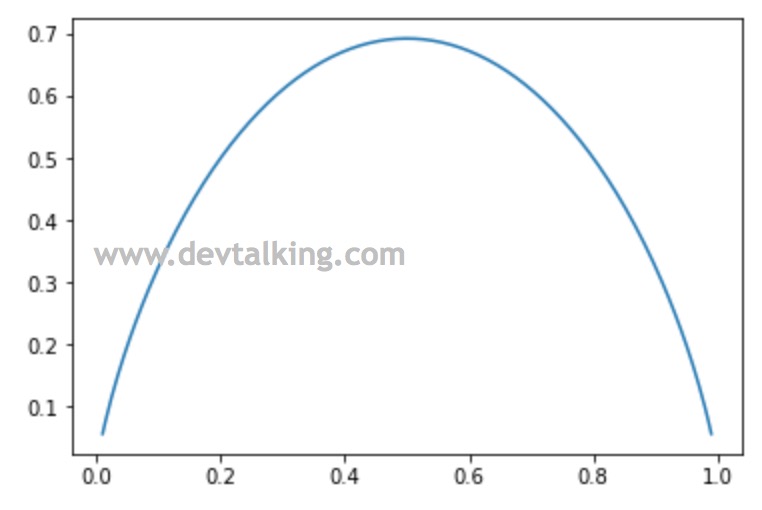
从图中可以看到,曲线是以横轴0.5为中心的抛物线。当比例$x$为0.5时,纵轴达到最大值,也就是信息熵达到了最大值,表示此时变量不确定性最大。因为两个类别各以0.5的比例出现,很难确定是哪个类型,所以不确定性大。
当以0.5为中心向两边延展后,可以看到信息熵在逐渐减小,意味着不确定性在减小。因为此时要么有一个比例在减小,要么有一个比例在增大。这两种情况都可以表明其中一种类别的比例在增大,所以更容易确定是哪种类别,故而不确定性减小。
使用信息熵寻找最优划分
之前我们有带着两个问题进入到了信息熵小节。那么这一节就来解答这两个问题:
- 决策树每个节点在哪个维度做划分?
- 某个维度在哪个值上做划分?
那么我们要做的事情就是找到一个维度和一个阈值,使得通过该维度和阈值划分后的信息熵最低,此时这个划分才是最好的划分。
用大白话解释一下就是,我们在所有数据中寻找到信息熵最低的维度和阈值,然后将数据划分为多个部分,再寻找划分后每部分信息熵最低的维度和阈值,继续划分下去,最终形成完整的决策树。这一节就来看看如何使用信息熵寻找最优划分。
划分函数
我们先定义一个划分函数,也就是相当于构建决策树根节点的作用:
import numpy as np |
举个例子来看看上面的划分函数:
# 构建一个五行四列的样本数据 |
计算信息熵函数
然后定义计算信息熵的函数:
from collections import Counter |
举个例子验证一下:
test_y = np.array([0, 0, 0, 0, 1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3]) |
寻找维度和阈值函数
最后我们来定义寻找最优信息熵、维度、阈值的函数,该函数的最基本思路就是遍历样本数据的每个维度,对该维度中每两个相邻的值求均值作为阈值,然后求出信息熵,最终找到最小的信息熵,此时计算出该信息熵的维度和阈值既是最优维度和最优阈值:
# 寻找最优信息熵 |
我们同样使用鸢尾花的数据进行验证,在验证之前,我们先将之前通过Scikit Learn的决策树求出的鸢尾花决策边界的图贴出来,做以对比:

from sklearn import datasets |
此时样本数据的第一个根节点的判断条件就求出来了,从上面的决策边界图中可以看到,第一次划分确实是从第0个维度,既横轴开始,以2.4左右为阈值进行的。我们来看看通过这个根节点划分后的数据是什么样的:
X_l1, X_r1, y_l1, y_r1 = split(X, y, best_d, best_v) |
从上面结果可以看到,经过第一个根节点划分后,对左侧数据求信息熵的结果为0,说明左侧的数据现在只有一个类型了。从上图也可以清晰的看到,以横轴2.4往左的区域全部是蓝色的点。那么对右侧而言,它的信息熵是0.69,说明对右侧还可以继续划分:
best_entropy2, best_d2, best_v2 = try_split(X_r1, y_r1) |
第二次划分以第一个维度上的1.75为阈值进行,这和上图中的纵轴的划分界限基本是一致的。再来看看划分后的结果:
X_l2, X_r2, y_l2, y_r2 = split(X_r1, y_r1, best_d2, best_v2) |
可以看到第二次划分后,两部分的信息熵都不为零,其实还可以对每部分再进行划分。不过在之前使用Scikit Learn的决策树划分时,我们将深度设为了2,所以就只划分到了目前的阶段,如果将深度设的更大的话,那么就会继续划分下去。在我们模拟寻找最优划分的过程中,就不再继续划分下去了,大家理解了划分过程就可以了。
申明:本文为慕课网liuyubobobo老师《Python3入门机器学习 经典算法与应用》课程的学习笔记,未经允许不得转载。