先来看一张真实的甜甜圈。

一共有三个特点：

• 甜甜圈腰部有一圈凹陷。
• 流下来的糖衣是上小下大的形状，这个和密度大的液体从上往下流的道理是一样的。
• 糖衣的边缘不是光滑的，是坑坑洼洼的。

这一节就是使用Blender的雕刻功能，将甜甜圈和糖衣的这几个特点刻画出来。

应用修改器

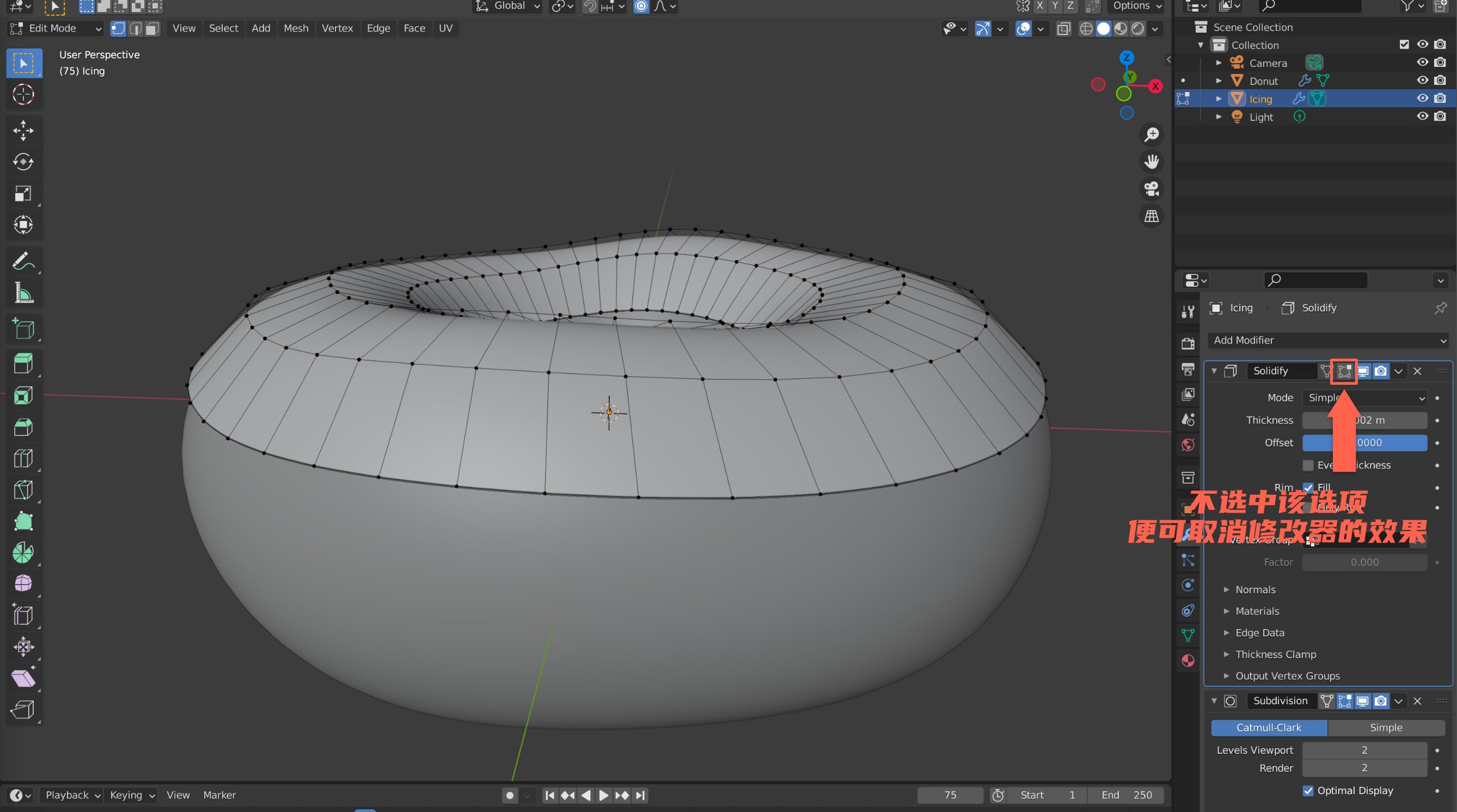
在开始之前，先回忆一下前面我们给甜甜圈和糖衣添加过修改器，但是我们并没有让修改器真正的生效，那么在雕刻前，需要将修改器的内容应用生效。在应用生效修改器之前，我们先对现在的白模复制一份，做个备份，因为修改器一旦生效后，整个拓扑都会发生变化。

选中甜甜圈和糖衣的白模，Shift + D复制一份，然后按下M键，新建一个集合，然后设置为不可见，相当于将复制出来的甜甜圈和糖衣做个备份。

目前甜甜圈的糖衣已经捏出了大体的样子，我们先来看看真正的甜甜圈上的糖衣是什么样的。

可以看到在烘培甜甜圈时，糖衣是会沿着甜甜圈流淌下去的，所以这个细节是需要我们刻画出来的。

完善糖衣

选中糖衣，进入编辑模式，先取消Solidify修改器的效果。

选中某个点，按下A键，即可选中该对象所有的点，Alt + A或Option + A是取消所有点的选中。

甜甜圈的白模胚子已经有了，然后我们开始做甜甜圈上面那一层糖衣的制作。基本思路是需要创建一个糖衣的白模，然后摞在甜甜圈白模上面，并且这个糖衣的白模需要有以下三个特点：

• 甜甜圈的糖衣一般只覆盖到甜甜圈上部1/3的范围。
• 糖衣的轮廓和甜甜圈上半部分完全一致。
• 糖衣需要一点点厚度，能看出来是甜甜圈上面覆盖了一层东西。

我们依照上面三个思路来进行制作。

制作糖衣白模

要想让糖衣的轮廓和甜甜圈完全一致，最好的做法就是复制甜甜圈上部1/3的部分。进入编辑模式，将视角切换到正前视图，然后用鼠标框选甜甜圈的上部1/3位置。

我们删除了正方体，添加了一个圆环，添加圆环后，左下角会出现该物体的各项属性，可以进行调整：

物体属性

先看Major Radius，它表示我们添加的物体的大小，Blender的默认单位是米，这里看到添加的圆环大小是1米，可以将它调整到一个甜甜圈的实际大小，可以直接5cm，Blender会自动换算单位。

从场景中的网格大小也可以对比出物体大小和视角远近的变化。如果想修改单位，可以在右侧的场景属性中进行设置。

Blender基本操作

和场景相关的基本操作

• 按住鼠标中键，可以基于原点旋转场景。
• 按住Shift+鼠标中键，移动场景。
• 按下```，出现8个选项的轮盘，鼠标快速移到对应的方位即可触发效果。

这8个选项分别是：

• Top：从上往下看的正交视图。
• Bottom：从下往上看的正交视图。
• Left：从左往右看的正交视图。
• Right：从右往左看的正交视图。
• Front：从物体正前方看的视图。
• Back：从物体正后方看的视图。
• View Camera：开启摄像机视图。
• View Selected：将视角拉近选中的物体。