决策边界
决策边界顾名思义就是需要分类的数据中,区分不同类别的边界,举个不恰当的例子,就像省的地界一样,你处在北京还是处在河北,全看你站在区分北京和河北的那条线的哪边。这节我们来看看使用逻辑回归算法如何绘制鸢尾花前两个分类的决策边界。
线性决策边界
再来回顾一下逻辑回归,我们需要找到一组$\theta$值,让这组$\theta$和训练数据相乘,然后代入Sigmoid函数,求出某个类别的概率,并且假设,当概率大于等于0.5时,分类为1,当概率小于0.5时,分类为0:
$$\hat p = \sigma(\theta^T X_b)=\frac 1 {1+e^{-\theta^{T}X_b}}$$
$$\hat y =\left\{
\begin{aligned}
1, \ \ \ \hat p \ge 0.5 \\
0, \ \ \ \hat p < 0.5 \\
\end{aligned}
\right.
$$
在Sigmoid函数那节解释过,当$t>0$时,$\hat p>0.5$。当$t<0$时,$\hat p<0.5$,因为$t= \theta^T X_b $,所以:
$$\hat y =\left\{
\begin{aligned}
1, \ \ \ \ \hat p \ge 0.5, \ \ \ \ \theta^T X_b \ge 0 \\
0, \ \ \ \ \hat p < 0.5, \ \ \ \ \theta^T X_b < 0 \\
\end{aligned}
\right.
$$
那么当$\theta^T X_b =0$时,理论上$\hat p$就是0.5,分类既可以为0,也可以为1。只不过我们在这里将$\hat p=0.5$是,分类假设为1。由此可见$\theta^T X_b =0$就是逻辑回归中的决策边界,并且是线性决策边界。
下面来解释一下为何说是线性决策边界。我们以前两个分类的鸢尾花为例,将$\theta^T X_b =0$展开得:
$$\theta_0 + \theta_1 X_1 + \theta_2 X_2=0$$
$\theta_0$就是截距,$\theta_1$和$\theta_2$是系数,这个公式绘制出来的是一条直线,这条直线就是能将鸢尾花数据的前两个分类区分开的直线,既线性决策边界。为了能方便的将这条直线绘制出来,我们对上面的公式做一下转换:
$$X_2 = \frac {-\theta_0 - \theta_1 X_1} {\theta_2}$$
下面我们在Jupyter Notebook中绘制出来看看:
import numpy as np |
上面的代码中可以看到,$\theta_0$,$\theta_1$和$\theta_2$都已经知道了。接下来要做的就是给定一组$X_1$然后通过上面的公式求出$X_2$,最后绘制出线性决策边界直线:
# 定义求X2的函数 |

不规则决策边界
目前我们实现的逻辑回归是使用线性回归来实现的,同样可以通过添加多项式项使决策边界不再是直线。同样,还有像KNN算法在多分类问题中决策边界必然都不是直线,而是不规则的决策边界,所以自然也无法通过一个线性方程来绘制。那么这一小节来看看如何绘制不规则决策边界。
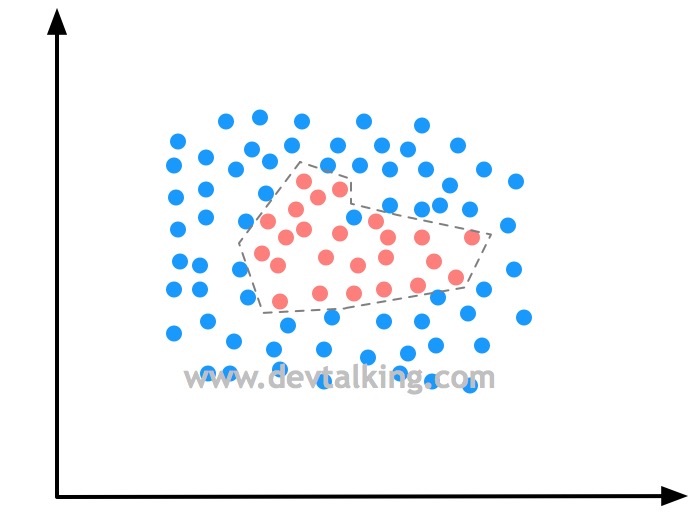
从上面的图中可以看出,红蓝点的区分界限并不是一条直线,而是一个不规则的形状,这就是不规则决策边界。那么绘制不规则决策边界的方法其实也很简单,就是将特征平面上的每一个点都用我们训练出的模型判断它属于哪一类,然后将判断出的分类颜色绘制出来,就得到了上图所示的效果,那么不规则决策边界自然也就出来了,这个原理类似绘制地形图的等高线,在同一等高范围内的点就是同一类。
等高线指的是地形图上高程相等的各点所连成的闭合曲线。
既然运用了等高线的原理,那么我们的绘制方法思路就很明了了:
def plot_decision_boundary(model, axis): |
我对这个方法中的几个函数做一下解释:
np.meshgrid()这个函数的作用是用给定坐标轴上的点在平面上画格,返回组成网格点的坐标矩阵。ravel()方法将高维数组降为一维数组。c_[]将两个数组以列的形式拼接起来,形成矩阵。
我用一幅图对上面的方法做以形象的说明:
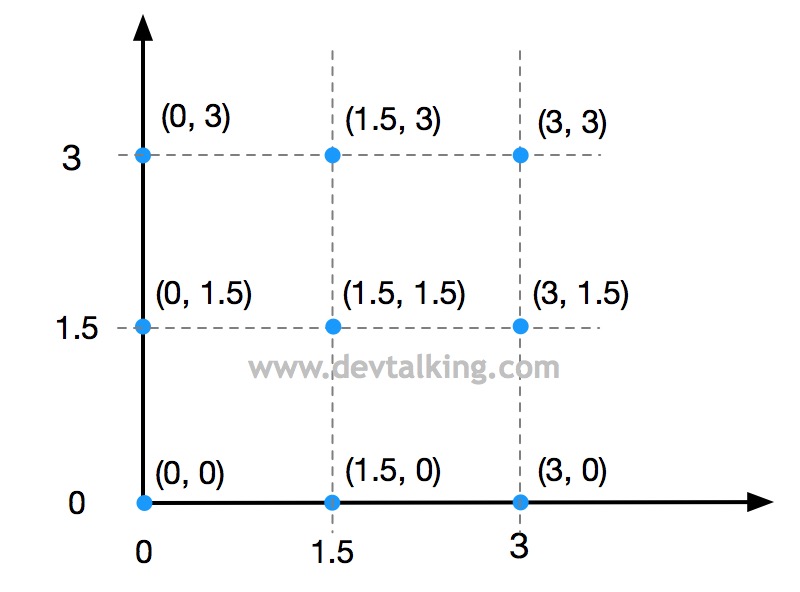
假设传给np.meshgrid()方法的两个坐标轴上共计六个点,然后返回由这六个点组成的网格的坐标矩阵,既网格相交点的坐标矩阵:
x0, x1 = np.meshgrid( |
因为返回的结果将这九个点的坐标分开了,所以通过np.c_[X0.ravel(), X1.ravel()]将这九个点的坐标合起来。
np.c_[x0.ravel(), x1.ravel()] |
然后通过训练好的逻辑回归模型对这九个点预测它们的分类,将预测出的分类作为等高区间。最后通过ListedColormap定义我们自己的色彩表,再使用Matplotlib的contourf函数将等高区域绘制出来,也就是将分类用颜色区分出来。contourf函数的前两个参数是确定点的坐标矩阵,第三个参数是高度,第四个参数是等高线的粗细度,第五个参数是色彩表。
下面我们来使用一下plot_decision_boundary方法:
plot_decision_boundary(log_reg, axis=[4, 7.5, 1.5, 4.5]) |
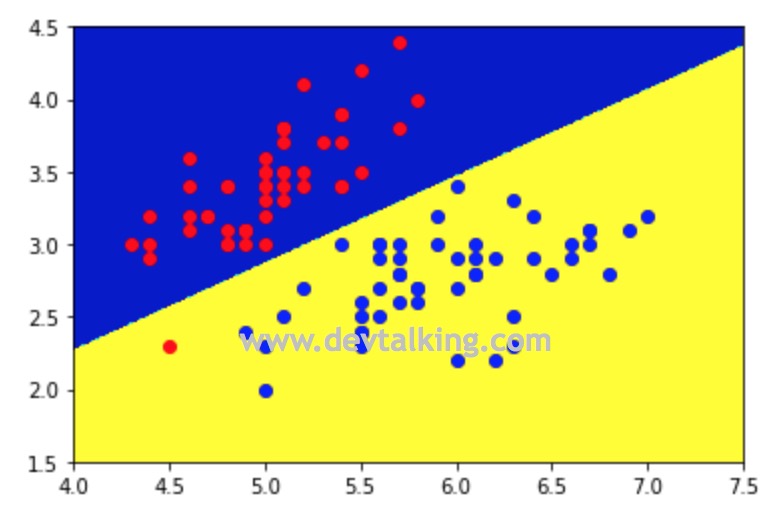
kNN的决策边界
因为kNN算法在解决二分类问题时是无法像逻辑回归算法那样推导出线性决策边界的公式的,所以我们使用绘制不规则决策边界的方式来看一下kNN算法的决策边界:
from sklearn.neighbors import KNeighborsClassifier |
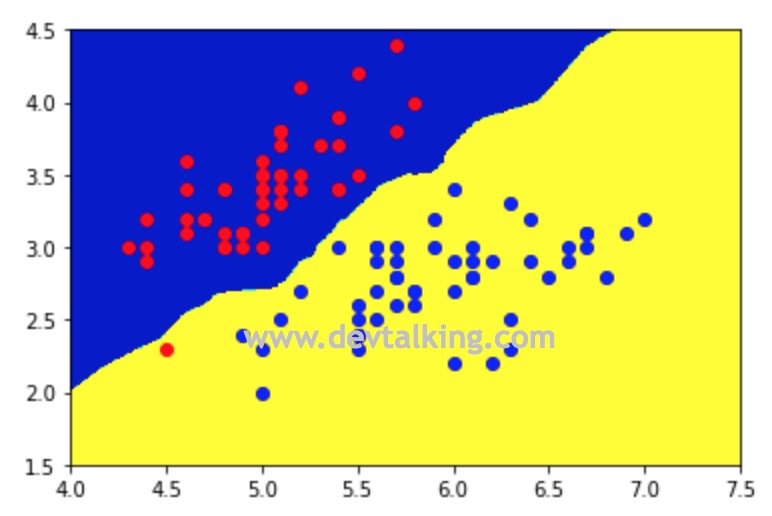
下面再来看看当kNN在解决多分类问题时的决策边界是怎样的:
knn_clf_all = KNeighborsClassifier() |
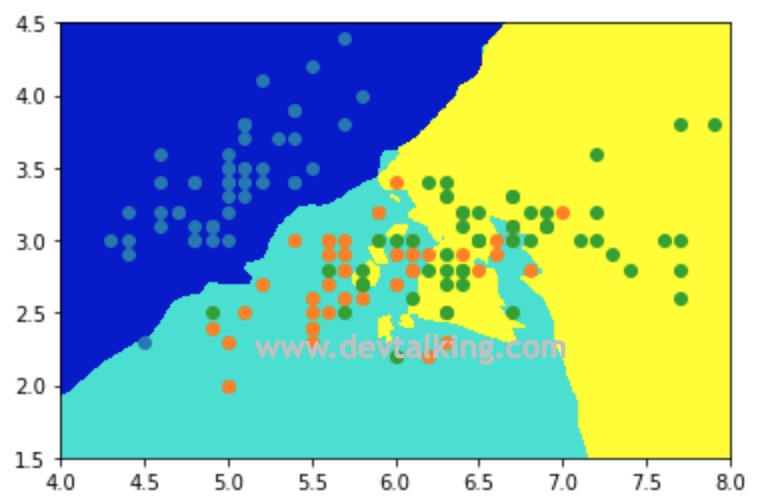
从上面的三分类不规则决策边界图中可以看到,在绿色区域里还有些黄色区域,这表示我们的kNN模型有过拟合的现象,也就是k值过小导致的。在第三篇笔记中讲kNN算法时讲过,k值越小,kNN的模型就越复杂。所以我们手动将k值调整为50,再看一下决策边界的情况:
knn_clf_all = KNeighborsClassifier(n_neighbors=50) |
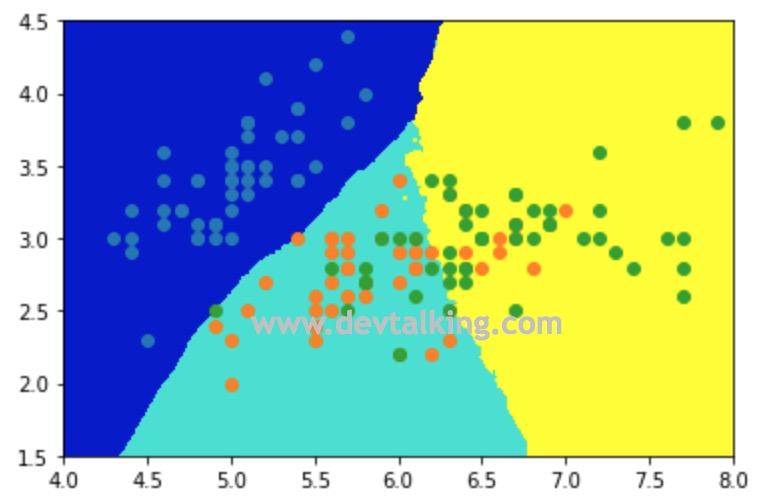
现在可以看到分类区域界限是相对比较规整清晰了。
逻辑回归中使用多项式特征
在讲逻辑回归中使用多项式特征前,先来举个例子看一下:
import numpy as np |

从上图可以看到,我们构建的样本数据,明显无法用一条直线将两个不同颜色的点区分开,我们使用上一节的方法来验证一下:
# 导入我们实现的逻辑回归方法训练模型 |
可以看到训练出的模型预测分数非常低。再来看看决策边界:
plot_decision_boundary(log_reg, axis=[-4, 3, -3, 3]) |

从图中可以看到,绘制出的线性决策边界是完全没办法区分样本数据中的两种类型的。
并且我们也清楚的知道,样本数据的决策边界应该是下图所示:

那么我们如何能得到一个圆形的决策边界呢?大家回忆一下,在几何中我们学过圆的标准方程应该是:
$$(x-a)^2 + (y-b)^2 = r^2$$
$a$和$b$是圆心坐标,$r$是半径。那如果我们将上图的圆看作是一个圆心在$(0, 0)$的圆,那么这个圆形的决策边界公式应该就是:
$$x^2 + y^2 -r^2 = 0$$
和逻辑回归的线性决策边界公式做一下对比:
$$\theta_1 X_1 + \theta_2 X_2 + \theta_0 = 0$$
是不是发现相当于给线性决策边界的特征增加幂次,再回想之前笔记中讲过的多项式回归,此时大家应该心中就了然了。那就是如果要让逻辑回归处理不规则决策边界分类问题,那么就运用多项式回归的原理,下面我们实现来看看:
# 用到了前面笔记中讲过的Pipeline |
可以看到使用多项式回归原理后,我们训练出的新的模型对样本数据的预测评分达到了98%。再来绘制一下决策边界看看:
plot_decision_boundary(ploy_log_reg, axis=[-4, 3, -3, 3]) |

现在圆形的决策边界就被绘制出来了,并且将样本数据的类型区分的很准确。
逻辑回归中使用模型正则化
上一节中,我们讲了使用多项式的方式使得逻辑回归可以解决非线性分类的问题,那么既然使用了多项式方法,那势必模型就会变的很复杂,继而产生过拟合的问题。所以和多项式解决回归问题一样,在逻辑回归中使用多项式也要使用模型正则化来避免过拟合的问题。
这一节我们使用Scikit Learn中提供的逻辑回归来看一下如何使用模型正则化。在这之前先来复习一下模型正则化。所谓模型正则化,就是在损失函数中加一个带有系数的正则模型,那么此时如果想让损失函数尽可能的小,就要兼顾原始损失函数和正则模型中的$\theta$值,从而做以权衡,起到约束多项式系数大小的作用。正则模型前的系数$\alpha$ 决定了新的损失函数中每一个$\theta$都尽可能的小,这个小的程度占整个优化损失函数的多少。
$$L(\theta)_{new} = L(\theta) + \alpha L_p$$
$L_p$范数请参见机器学习笔记九之交叉验证、模型正则化 。
但是这种方式有一个问题,那就是可以刻意回避模型正则化,也就是将$\alpha$取值为0的时候。所以还有另一种模型正则化的方式是将这个系数加在原始损失函数前面,这种情况的话相当于正则模型前的系数永远是1,无论如何都要进行模型正则化。
$$L(\theta)_{new} = CL(\theta) + L_p$$
Scikit Learn中的逻辑回归就自带这种形式的模型正则化,下面我们来看一下:
import numpy as np |

样本数据构建好了,我们先用逻辑回归对其进行分类预测看看准确度:
from sklearn.model_selection import train_test_split |
当模型训练完后,我们在返回内容中可以看到两个超参数C和penalty,前者就是前面讲到的原始损失函数前的系数,后者就是正则模型,逻辑回归中这两个超参数的默认值是1和$L_2$范式正则模型,也就是LASSO正则模型。
log_reg.score(X_test, y_test) |

可以看到用线性逻辑回归训练出的模型准确度只有80%,并且线性决策边界无法很好的区分两种分类。下面我们再用多项式逻辑回归训练模型看看:
from sklearn.preprocessing import PolynomialFeatures |
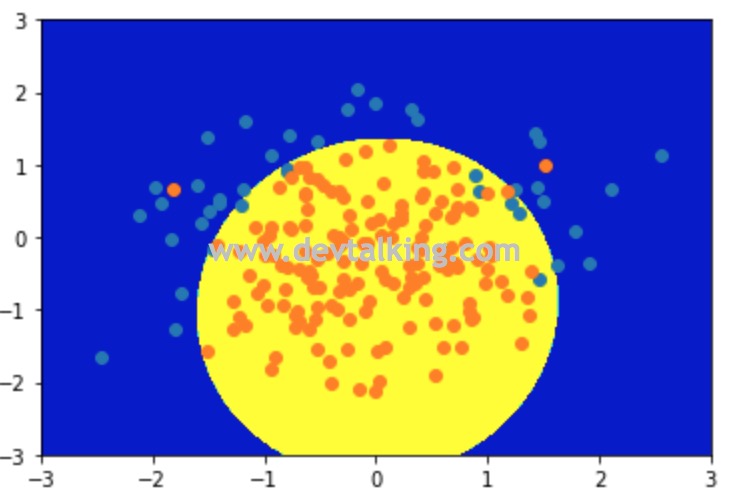
可以看到当使用多项式逻辑回归后,模型准确度达到了94%,不规则决策边界也很好的区分了两种类型。下面我们增加多项式的复杂度,再来看看:
ploy_log_reg2 = PolynomialLogisiticRegression(degree=20, C=1) |
可以看到当degree增大到20时,模型准确率有所下降,因为我们的样本数据量比较小,所以过拟合的现象不是很明显,我们绘制出决策边界看看:
plot_decision_boundary(ploy_log_reg2, axis=[-3, 3, -3, 3]) |

从决策边界上能很明显的看到过拟合的状态。下面我们来调整C这个系数,让正则模型来干预整个损失函数中$\theta$的大小,然后再看看模型准确率和决策边界:
ploy_log_reg3 = PolynomialLogisiticRegression(degree=20, C=0.1) |
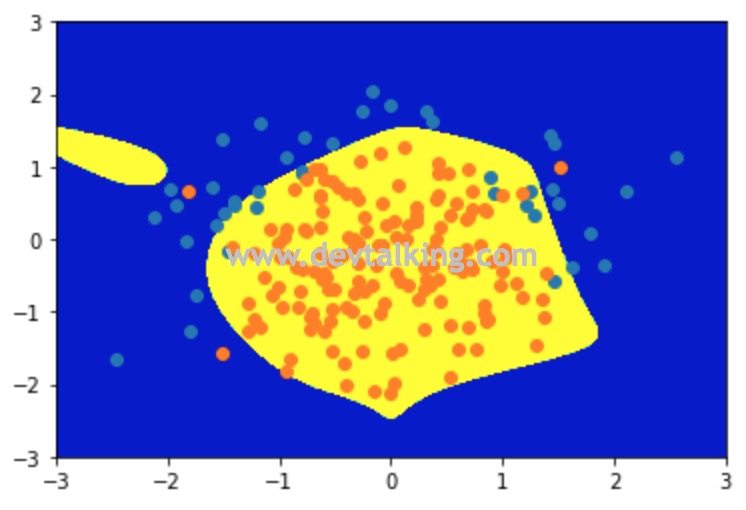
可以看到当正则模型进行干预后,模型的准确率有所提升,决策边界也比之前好了许多。这就是逻辑回归中的模型正则化。
逻辑回归解决多分类问题
在前面的章节中,对逻辑回归的应用一直是在二分类问题中进行的。这一节来讲讲能够让逻辑回归解决多分类问题的方法。
OvR
所谓OvR就是One vs Rest的缩写,从字面上来讲是一对剩余的所有的意思。那么我们通过一系列示图来解释一下OvR:

假设有四个分类,如上图所示,如果One指的是蓝色的点,那么剩余的红色、绿色、黄色三个点就是Rest,也就是我们选取一个类别,把其他剩余的类别称之为剩余类别:

这样就把一个四分类问题转换成了二分类问题,现在我们就可以使用逻辑回归算法预测再来一个点时它属于蓝色点的概率和属于剩余点的概率。
同理,这个过程也可以在其他颜色的点上进行,如果是上图的四分类问题,那么就可以拆分为四个二分类问题:

然后对新来的点分别在这四个二分类问题中计算概率,也就是N个类别就进行N次分类,最后选择分类概率最高的那个二分类,这样就可以判断这个新点的类别了。
OvO
所谓OvO就是One vs One的缩写,从字面上来讲是一对一的意思。那么我们同样通过一系列示图来解释一下OvO:

还是假设有四个分类,将其中的每两个分类单独拿出来处理,这样就一共有六组二分类问题,然后对新来的点分别在这六个二分类问题中计算概率,最后选择分类概率最高的那个二分类,这样就可以判断这个新点的类别了,这就是OvO方式。很明显OvO方式的时间复杂度要比OvR高很多,但是准确率也高很多,因为每次都是在绝对的二分类中对新来的样本数据进行概率计算
Scikit Learn中的逻辑回归
这一节我们来看看Scikit Learn中封装的逻辑回归。我们使用鸢尾花的样本数据:
import numpy as np |
从打印结果中我们能看到有一个属性叫multi_class它的值为ovr,其实Scikit Learn中的逻辑回归是自带OvR和OvO能力的,默认使用OvR。另外还需要注意solver属性,这个属性指定了逻辑回归使用的算法,如果使用了ovr,则对应的算法是liblinear。
log_reg1 = LogisticRegression(multi_class='multinomial', solver='newton-cg') |
如果要使用OvO方式,需要显示的传入multi_class和solver这两个参数,对应OvO的算法是newton_cg,这里就不对这两个算法做详细解释了,可以看看Scikit Learn的官网说明。
OvO和OvR类
除了在逻辑回归中自带了OvR和OvO方式以外,Scikit Learn还专门提供了单独的OvR和OvO的类,只要传入一个二分类器,就可以运用OvR和OvO的原理来解决多分类问题了:
from sklearn.multiclass import OneVsRestClassifier |
总结
这两篇笔记主要讲了逻辑回归,这是解决分类问题应用很广泛的一个算法,它拓展了线性回归算法,将估算概率的方式将回归问题转换为了分类问题。下一篇笔记将讨论如何更好的评价分类问题的准确度。
申明:本文为慕课网liuyubobobo老师《Python3入门机器学习 经典算法与应用》课程的学习笔记,未经允许不得转载。