这篇笔记主要介绍线性回归算法，对在第一篇笔记中介绍过的线性回归算法进行实现。kNN算法主要解决的是分类问题，并且它的结果不具备良好的解释性。线性回归算法主要解决回归问题，它的结果具有良好的可解释性，和kNN算法的介绍过程一样，线性回归算法也蕴含了机器学习中很多重要的思想，并且它是许多强大的非线性模型的基础。

简单线性回归

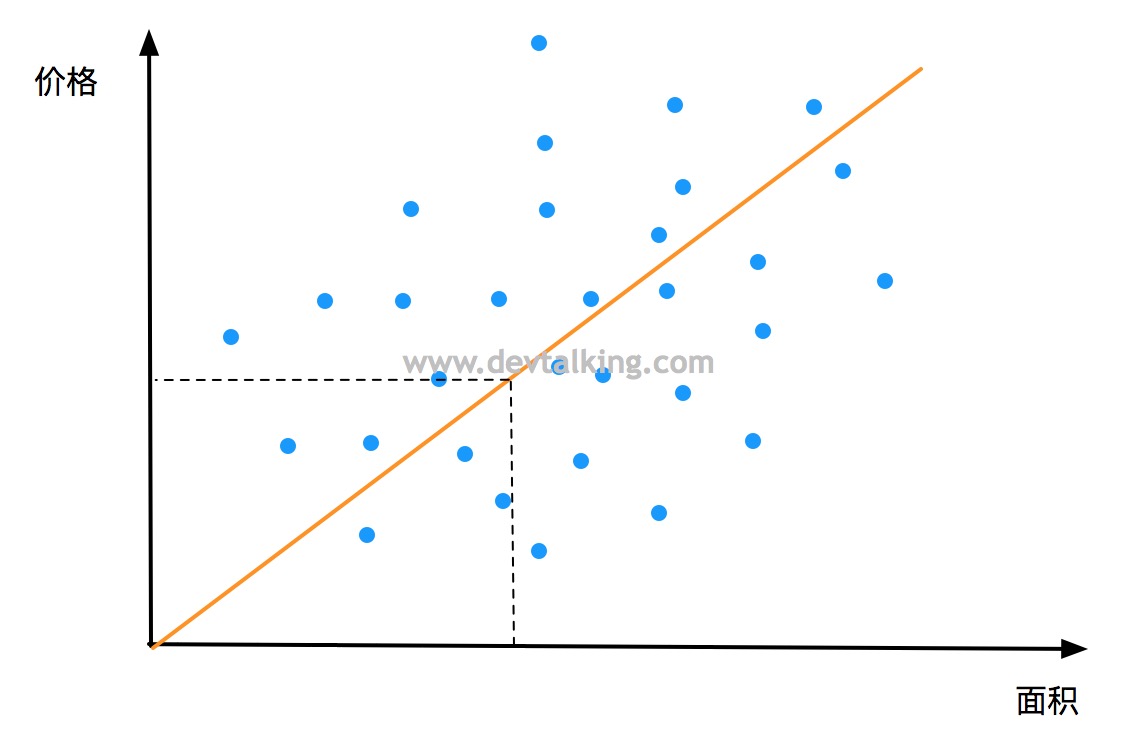
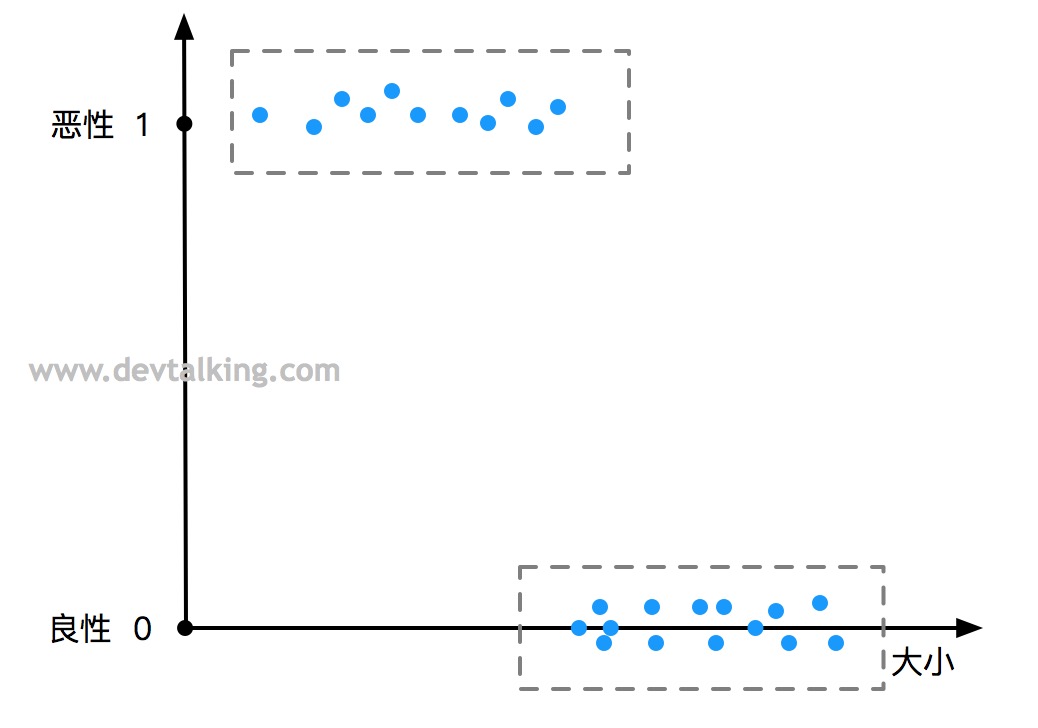
在第一篇笔记中，我们举过房屋面积大小和价格例子，将其绘制在二维坐标图上，横轴表示房屋面积，纵轴表示房屋价格，这里样本特征数据只有一个，那就是房屋面积，而在kNN算法的分类问题中，二维坐标图上横纵轴表示的都是样本特征数据，这是一个比较明显的区别。如果线性回归问题要在图中表示两种样本特征数据的话就需要三维空间坐标来表示。我们一般将只有一种样本特征数据的线性回归问题称为简单线性回归问题。

回顾线性回归

线性回归其实就是寻找一条直线，最大程度的拟合样本特征和样本输出标记之间的关系。

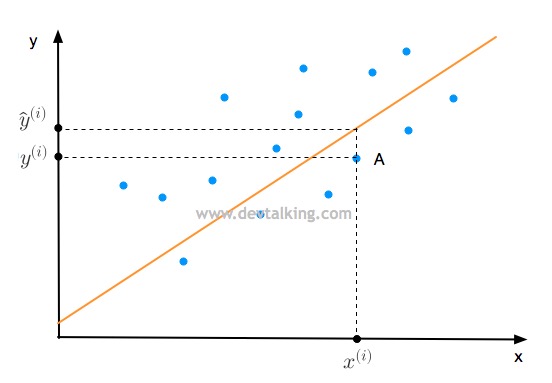
我们来看上面这张图，大家知道直线的方程是$y=ax+b$，那么点A肯定是在一条直线上，该条直线方程为$y^{(i)}=ax^{(i)}+b$，那么点A的横轴值为$x^{(i)}$，既是A的样本特征值，纵轴值为$y^{(i)}$，既是A的样本输出值。我们假设图中的红线就是拟合直线，方程为$\hat y^{(i)}=ax^{(i)}+b$，也就是将$x^{(i)}$代入这条红线，会得到一个预测的纵轴值$\hat y^{(i)}$。我们希望真值$y^{(i)}$和预测值$\hat y^{(i)}$的差值越小，说明我们的拟合直线拟合的越好。

因为差值有正有负，为了保证都是正数，所以将差值进行平方，之所以不用绝对值，是为了方便求导数。

方程求导的知识可参阅 《机器学习笔记一之机器学习定义、导数、最小二乘》 。

$$ (y^{(i)} - \hat y^{(i)})^2 $$

将所有样本特征都考虑到，既将所有真值和预测值的差值求和：

$$ \sum_{i=1}^m(y^{(i)} - \hat y^{(i)})^2 $$

将$ax^{(i)}+b$代入上面的公式就得到：

$$\sum_{i=1}^m(y^{(i)} - ax^{(i)}-b)^2$$

上面的公式我们称为损失函数（Loss Function），损失函数值越小，我们的拟合直线越好。在Loss函数中，$a$和$b$是变量，所以我们要做的就是找到使Loss函数值最小的$a$和$b$。这个套路是近乎所有参数学习算法常用的套路，既通过分析问题，确定问题的损失函数，通过最优化损失函数获得机器学习的模型。像线性回归、多项式回归、逻辑回归、SVM、神经网络等都是这个套路。

上一篇笔记主要介绍了NumPy，Matplotlib和Scikit Learn中Datasets三个库的用法，以及基于欧拉定理的kNN算法的基本实现。这一篇笔记的主要内容是通过PyCharm封装kNN算法并且在Jupyter Notebook中调用，以及计算器算法的封装规范，kNN的k值如何计算，如何使用Scikit Learn中的kNN算法，还有机器学习算法中的一些主要概念，比如训练数据集、测试数据集，分类准确度，超参数，数据归一化。另外会具体用代码实现第一篇笔记中介绍过的线性回归算法。

封装kNN算法

上一篇笔记中我们对kNN算法在Jupyter Notebook中进行了实现，但是想要复用这个算法就很不方便，所以我们来看看如何在PyCharm中封装算法，并且在Jupyter Notebook中进行调用。

PyCharm的配置这里我就不再累赘，如图所示，我们创建了一个Python文件kNN.py，然后定义了kNNClassify方法，该方法有4个参数，分别是kNN算法的k值，训练样本特征数据集XTrain，训练样本类别数据集yTrain，预测特征数据集x。该方法中的实现和在Jupyter Notebook中实现的一模一样，只不过加了三个断言，让方法的健壮性更好一点。我们给出N维欧拉定理：

$$ \sqrt {\sum_{i=1}^n(x_i^{(a)}-x_i^{(b)})^2} $$

# kNN.py
import numpy as np
from math import sqrt
from collections import Counter

def kNNClassify(k, XTrain, yTrain, x):

	assert 1 <= k <= XTrain.shape[0], "k 的取值范围不正确"
	assert XTrain.shape[0] == yTrain.shape[0], "训练样本数据行数应该与训练结果集行数相同"
	assert XTrain.shape[1] == x.shape[0], "训练样本数据特性个数应该与被预测数据特性个数相同"

	distances = [sqrt(np.sum((xTrain - x) ** 2)) for xTrain in XTrain]
	nearest = np.argsort(distances)

	topKy = [yTrain[i] for i in nearest[:k]]
	votes = Counter(topKy)

	return votes.most_common(1)[0][0]

这样我们就在PyCharm中封装好了kNN算法的方法，我们再来看看如何在Jupyter Notebook中调用封装好的方法呢，这就需要使用%run这个命令：

import numpy as np

raw_data_X = [[3.393533211, 2.331273381],
			  [3.110073483, 1.781539638],
			  [1.343808831, 3.368360954],
			  [3.582294042, 4.679179110],
			  [2.280362439, 2.866990263],
			  [7.423436942, 4.696522875],
			  [5.745051997, 3.533989803],
			  [9.172168622, 2.511101045],
			  [7.792783481, 3.424088941],
			  [7.939820817, 0.791637231]
			 ]
raw_data_y = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]

XTrain = np.array(raw_data_X)
yTrain = np.array(raw_data_y)

x = np.array([8.093607318, 3.365731514])

# 使用%run命令可以引入Python文件，并可使用该Python文件中定义的属性和方法
%run ../pycharm/kNN.py
predicty = kNNClassify(6, XTrain, yTrain, x)
predicty
# 结果
1

NumPy

NumPy是Python中的一个类库，它支持高阶维度数组（矩阵）的创建及各种操作、运算，是我们在机器学习中经常会使用的一个类库。这一节再看一些NumPy的矩阵用法。

numpy.random

NumPy也提供了生成随机数和随机元素数组的方法，我们来看一下：

# 生成从0到10之间的随机数
np.random.randint(0, 10)
# 结果
3

# 生成元素从0到10，一共4个随机元素的数组
np.random.randint(0, 10, size=4)
# 结果
array([4, 7, 8, 1])

# 生成元素随机从0到10，3行5列的矩阵
np.random.randint(0, 10, size=(3, 5))
# 结果
array([[6, 9, 7, 0, 9],
	   [7, 4, 8, 7, 8],
	   [4, 4, 9, 7, 2]])

如果我们希望每次使用随机方法生成的结果都是一样的，一般调试时候有这个需求，此时NumPy的random()方法也提供了方便简单的方式，既随机种子的概念：

# 生成随机矩阵前给定一个种子
np.random.seed(123)
# 然后生成随机矩阵
np.random.randint(0, 10, size=(4, 5))
# 结果
array([[2, 2, 6, 1, 3],
	   [9, 6, 1, 0, 1],
	   [9, 0, 0, 9, 3],
	   [4, 0, 0, 4, 1]])
	   
# 再次生成随机矩阵时，只要传入相同的种子，就可以得到相同结果的矩阵
np.random.seed(123)
np.random.randint(0, 10, size=(4, 5))
# 结果
array([[2, 2, 6, 1, 3],
	   [9, 6, 1, 0, 1],
	   [9, 0, 0, 9, 3],
	   [4, 0, 0, 4, 1]])
	   
# 默认范围是从0.0到1.0，返回值为float型
np.random.random()
# 结果
0.18249173045349998

# 传入的参数是数组的大小
np.random.random(10)
# 结果
array([ 0.17545176,  0.53155137,  0.53182759,  0.63440096,  0.84943179,
		0.72445532,  0.61102351,  0.72244338,  0.32295891,  0.36178866])
		
# 创建4行5列，元素值的范围从0.0到1.0的矩阵
np.random.random((4, 5))
# 结果
array([[ 0.22826323,  0.29371405,  0.63097612,  0.09210494,  0.43370117],
	   [ 0.43086276,  0.4936851 ,  0.42583029,  0.31226122,  0.42635131],
	   [ 0.89338916,  0.94416002,  0.50183668,  0.62395295,  0.1156184 ],
	   [ 0.31728548,  0.41482621,  0.86630916,  0.25045537,  0.48303426]])

指定均值和标准差生成随机数数组或矩阵

我们先来看看均值、方差、标准差的概念。均值很好理解，就是所有样本数据的平均值，描述了样本集合的中间点：

$$ \overline X=\frac{\sum_{i=1}^nX_i}n $$

方差是衡量样本点和样本期望值相差的度量值：

$$ S^2 = \frac{\sum_{i=1}^n(X_i-\overline X)^2} n $$

标准差描述的是样本集合的各个样本点到均值的距离之平均：

$$ S = \sqrt {\frac{\sum_{i=1}^n(X_i-\overline X)^2} n } $$

标准差也就是对方差开根号。举个例子，[0, 8, 12, 20]和[8, 9, 11, 12]，两个集合的均值都是10，但显然两个集合的差别是很大的，计算两者的标准差，前者是8.3后者是1.8，显然后者较为集中，标准差描述的就是这种散布度或者叫做波动大小。综上，方差的意义在于描述随机变量稳定与波动、集中与分散的状况。标准差则体现随机变量取值与其期望值的偏差。

矩阵

因为在机器学习中，一些概念、算法都涉及到矩阵的知识，比如训练数据集通常都是以矩阵的方式存在，所以在这里首先介绍一下矩阵的概念。

基本概念

在数学概念中，一个$m \times n$的矩阵指的是一个由$m$行$n$列元素排列而成的矩形阵列。用大白话解释就是将一些元素排列成若干行，每行放上相同数量的元素，就是一个矩阵。矩阵里的元素可以是数字、符号或数学式，比如下面这个$A$矩阵就是一个四行两列的矩阵：
$$ A=\begin{bmatrix}
1&2\\
3&4\\
5&6\\
7&8\\
\end{bmatrix}$$

一个矩阵$A$从左上角数起的第$i$行第$j$列上的元素称为第$i$，$j$项，通常记为$A_{i,j}$、$A_{ij}$或者$A_{[i,j]}$，那么上面的$A$矩阵中$A_{3,2}=6$。如果我们不知道矩阵$A$的具体元素，通常将其表示为$A=[a_{ij}]_{m \times n}$，如果$A$的元素可以写成与行$i$和列$j$有关的统一函数$f$，那么也可以用$A=[f(i,j)]_{m \times n}$来表示。

矩阵的基本运算

矩阵的最基本运算包括矩阵加（减）法、数乘、转置、矩阵乘法运算。

加减法运算

$m \times n$矩阵$A$和$B$的和（差）$A \pm B$也是一个$m \times n$矩阵，其中每个元素是$A$和$B$相应元素的和（差），即$ (A \pm B)_{ij}=A_{ij} \pm B_{ij} $，其中$1 \le i \le m$，$1 \le j \le n$。举个例子：

$$ \begin{bmatrix}
1&2&3\\
4&5&6\\
\end{bmatrix} + \begin{bmatrix}
6&5&4\\
3&2&1\\
\end{bmatrix} = \begin{bmatrix}
1+6 & 2+5 & 3+4 \\
4+3 & 5+2 & 6+1 \\
\end{bmatrix}=\begin{bmatrix}
7&7&7\\
7&7&7\\
\end{bmatrix}
$$

数乘运算

标量$c$与$m \times n$的矩阵$A$的数乘也是一个$m \times n$的矩阵$cA$，它的每个元素是矩阵$A$的相应元素与$c$的乘积$(cA)_{ij}=c \cdot A_{ij}$，举个例子：

$$
2 \cdot \begin{bmatrix}
1&2&3\\
4&5&6\\
\end{bmatrix}=\begin{bmatrix}
2 \cdot 1 & 2 \cdot 2 & 2 \cdot 3 \\
2 \cdot 4 & 2 \cdot 5 & 2 \cdot 6 \\
\end{bmatrix}=\begin{bmatrix}
2&4&6\\
8&10&12\\
\end{bmatrix}
$$

机器学习的定义

• 非正式定义：在不直接针对问题进行编程的情况下，赋予计算机学习能力的一个研究领域。
• 正式定义：对于一个计算机程序来讲，给他一个任务T和一个性能测量方法P，如果在经验E的影响下P对T的测量结果得到了改进，那么就说该程序从E中得到了学习。

举个机器下棋的例子，经验E对应着程序不断和自己下棋的经历，任务T是下棋，性能测量方法P可以是它在和人类棋手对弈的胜率。如果说机器与人类棋手对应的胜率不断提高，那说明机器从自己和自己下棋的过程中得到了学习。

机器学习四大内容简述

• 监督学习（Supervised Learning）
• 学习理论（Learning Theory）
• 无监督学习（Unsupervised Learning）
• 强化学习（Reinforcement Learning）

监督学习（Supervised Learning）

如上图所示，描述了假定城市区域的房屋面积与售价的关系。横坐标是房屋面积，纵坐标是售价。如果我想在横轴随意取一个面积，就希望知道它的售价，那么就需要一个方法通过面积确定售价。图中的方法是通过一条标准线来找到对应的售价。那么这条线要如何得来呢？

在这个示例中，我们已经给出了若干房屋面积和售价的数据集，即已经告知了机器若干问题和答案。机器通过这些数据集中面积和售价的关系，自我学习从而得出这条线，这种学习类型就属于监督学习类型。

因为这种场景中的数据集取值都是连续的，所以这类问题都可以归为线性回归的问题。

如上图所示，描述了肿瘤大小与恶性良性的关系。横坐标是肿瘤的大小，纵坐标表示恶性或良性，与连续的房屋售价不同的是，这里的纵坐标只有两个值0或1。

这个示例中，我们同样给出了一组肿瘤大小与恶性良性的数据集，我们希望机器通过这组答案数据集自我学习然后有能力通过肿瘤大小判断出恶性或良性。当然这里只是示例，实际中会有很多其他的横轴指标值用于判断学习。

该示例中这种离散的数值问题可以归为分类的问题。

学习理论（Learning Theory）

任何具体的方式方法背后都有一个或多个理论进行支撑，机器学习也不例外。

这一大块的内容贯穿整个机器学习，包括人工智能和机器学习正式诞生之前的定理证明，理解为什么学习型算法是有效的。每种学习型算法需要多少训练数据，比如上面的房屋售价示例到底需要多少房屋的样本。以及机器学习渗透在我们生活中的真实应用场景等等。

无监督学习（Unsupervised Learning）

如果我现在有一组不知道任何信息的数据集，然后需要机器进行分析然后给出这组数据集中的几种共性或者相似的结构，将其聚类，这个方式就称之为无监督学习。即我们不会提供机器问题和答案，只提供数据，需要机器自我学习和分析找出共性进行聚类。

无监督学习的应用场景很多，当下流行的各种P图软件都或多或少的用到了这类算法，比如图的修复功能，抠图功能，像素化等一些滤镜都是对像素的聚类。还有声音驳杂功能，从嘈杂的声音中提取出有用的声音等。

强化学习（Reinforcement Learning）

强化学习是机器学习的精髓，更贴近机器的自我学习，用在不能通过一次决策下定论的情形中，比如分析病人肿瘤病情的例子，通过监督学习，我们给定了确切的答案，不是良性就是恶性，即我们做的决策要么对，要么错。但在强化学习中，在一段时间内会机器做出一系列决策。比如我们编写一个程序让一架无人机做出一系列特技表演动作，这种场景就不是一次决策能实现的了的。

那么强化学习究竟是什么？在它背后有一个称为回报函数的概念。比如我们训练宠物狗坐下、握手等行为，每当小狗做出的正确的行为，我们都会给小狗奖励，比如摸摸头进行鼓励或者给一块小骨头。渐渐的小狗就知道做出怎样的行为有奖励，怎样的行为没有奖励，即学会了坐下和握手的行为。这就很类似强化学习的理论，我们需要找到一种方式，来定义我们想要什么，如何定义一个好的行为和一个坏的行为，然后就需要一个合适的学习型算法来获得更多的回报和更少的惩罚。