机器学习的定义
- 非正式定义:在不直接针对问题进行编程的情况下,赋予计算机学习能力的一个研究领域。
- 正式定义:对于一个计算机程序来讲,给他一个任务T和一个性能测量方法P,如果在经验E的影响下P对T的测量结果得到了改进,那么就说该程序从E中得到了学习。
举个机器下棋的例子,经验E对应着程序不断和自己下棋的经历,任务T是下棋,性能测量方法P可以是它在和人类棋手对弈的胜率。如果说机器与人类棋手对应的胜率不断提高,那说明机器从自己和自己下棋的过程中得到了学习。
机器学习四大内容简述
- 监督学习(Supervised Learning)
- 学习理论(Learning Theory)
- 无监督学习(Unsupervised Learning)
- 强化学习(Reinforcement Learning)
监督学习(Supervised Learning)
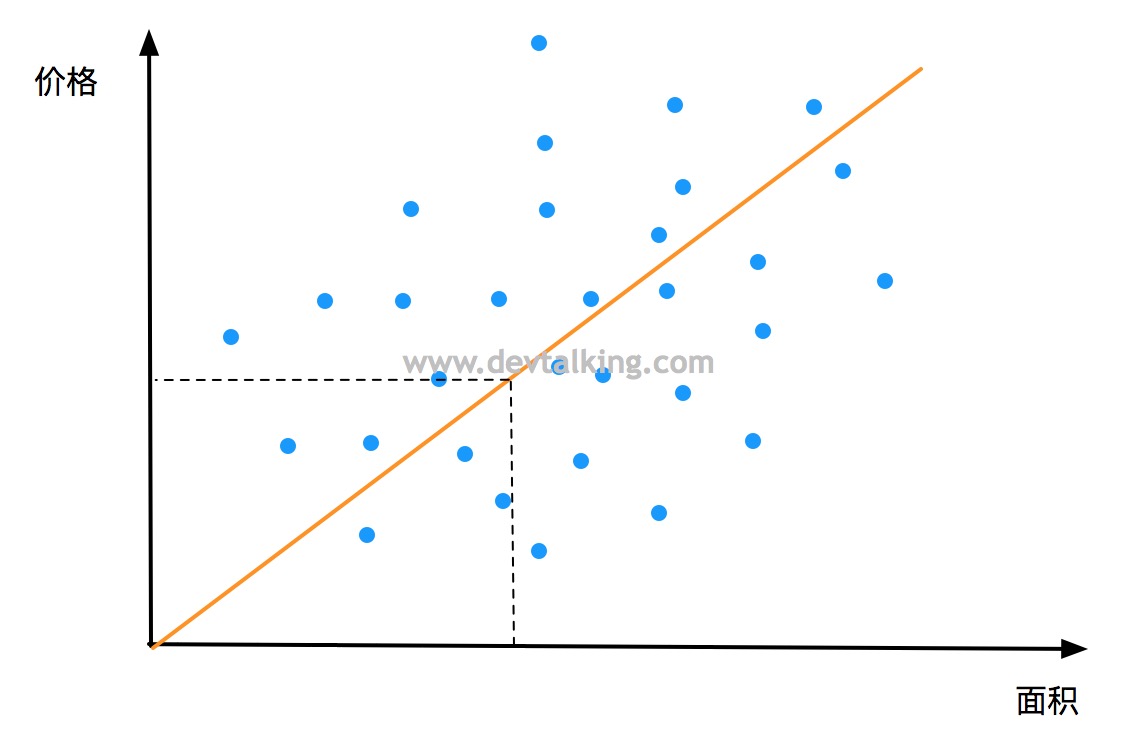
如上图所示,描述了假定城市区域的房屋面积与售价的关系。横坐标是房屋面积,纵坐标是售价。如果我想在横轴随意取一个面积,就希望知道它的售价,那么就需要一个方法通过面积确定售价。图中的方法是通过一条标准线来找到对应的售价。那么这条线要如何得来呢?
在这个示例中,我们已经给出了若干房屋面积和售价的数据集,即已经告知了机器若干问题和答案。机器通过这些数据集中面积和售价的关系,自我学习从而得出这条线,这种学习类型就属于监督学习类型。
因为这种场景中的数据集取值都是连续的,所以这类问题都可以归为线性回归的问题。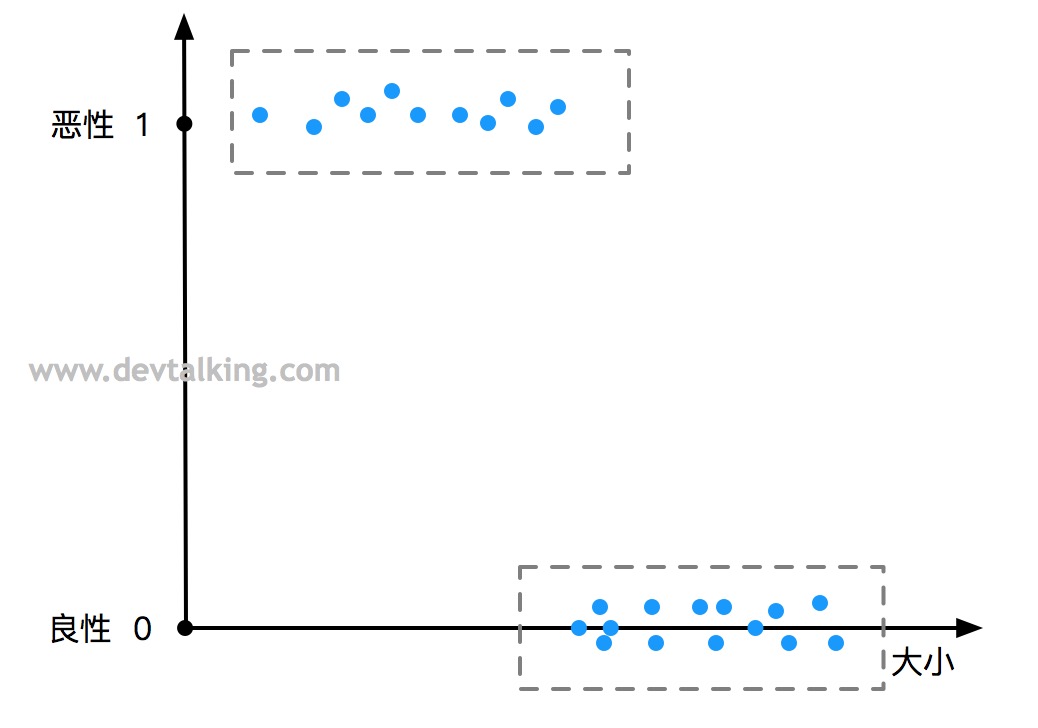
如上图所示,描述了肿瘤大小与恶性良性的关系。横坐标是肿瘤的大小,纵坐标表示恶性或良性,与连续的房屋售价不同的是,这里的纵坐标只有两个值0或1。
这个示例中,我们同样给出了一组肿瘤大小与恶性良性的数据集,我们希望机器通过这组答案数据集自我学习然后有能力通过肿瘤大小判断出恶性或良性。当然这里只是示例,实际中会有很多其他的横轴指标值用于判断学习。
该示例中这种离散的数值问题可以归为分类的问题。
学习理论(Learning Theory)
任何具体的方式方法背后都有一个或多个理论进行支撑,机器学习也不例外。
这一大块的内容贯穿整个机器学习,包括人工智能和机器学习正式诞生之前的定理证明,理解为什么学习型算法是有效的。每种学习型算法需要多少训练数据,比如上面的房屋售价示例到底需要多少房屋的样本。以及机器学习渗透在我们生活中的真实应用场景等等。
无监督学习(Unsupervised Learning)
如果我现在有一组不知道任何信息的数据集,然后需要机器进行分析然后给出这组数据集中的几种共性或者相似的结构,将其聚类,这个方式就称之为无监督学习。即我们不会提供机器问题和答案,只提供数据,需要机器自我学习和分析找出共性进行聚类。
无监督学习的应用场景很多,当下流行的各种P图软件都或多或少的用到了这类算法,比如图的修复功能,抠图功能,像素化等一些滤镜都是对像素的聚类。还有声音驳杂功能,从嘈杂的声音中提取出有用的声音等。
强化学习(Reinforcement Learning)
强化学习是机器学习的精髓,更贴近机器的自我学习,用在不能通过一次决策下定论的情形中,比如分析病人肿瘤病情的例子,通过监督学习,我们给定了确切的答案,不是良性就是恶性,即我们做的决策要么对,要么错。但在强化学习中,在一段时间内会机器做出一系列决策。比如我们编写一个程序让一架无人机做出一系列特技表演动作,这种场景就不是一次决策能实现的了的。
那么强化学习究竟是什么?在它背后有一个称为回报函数的概念。比如我们训练宠物狗坐下、握手等行为,每当小狗做出的正确的行为,我们都会给小狗奖励,比如摸摸头进行鼓励或者给一块小骨头。渐渐的小狗就知道做出怎样的行为有奖励,怎样的行为没有奖励,即学会了坐下和握手的行为。这就很类似强化学习的理论,我们需要找到一种方式,来定义我们想要什么,如何定义一个好的行为和一个坏的行为,然后就需要一个合适的学习型算法来获得更多的回报和更少的惩罚。
监督学习
线性回归
线性回归是监督学习中相对简单也但很实用的一个数学方法,它是用于确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。我们先从一元线性回归看起。
一元线性回归顾名思义只包括一个自变量和一个因变量,且二者的关系可用一条直线来近似表示,比如上文中的卖房示例,假设我们的分析数据如下表所示:
这组数据是链家网站望京二手房的数据,如果把这些数据画在二维坐标内,就可以得到一个散点图,就像上文图一所示,如果我们想得知房屋面积和售价的关系,就可以利用一元线性回归来画出一条拟合直线。
如何画出拟合直线
首先我们知道一元线性函数的表达式为$ f(y) = ax + b $,该函数可以在二维坐标系内画出一条直线,并且$y$的值随$x$的值变化而变化,既$x$是自变量,$y$是因变量。假设上面给出的数据房屋面积为$x$,售价为$y$,那么每一个实际的$x$值都会有一个实际的$y$值。那么对于我们要画出的拟合直线来讲,每一个实际的$x$值都会有一个通过拟合直线预测而来的$y$值,我们期望的结果是每个$y$的实际值与预测值的差的平方和最小,也就是预测出的值和真实的值差距越小,那么认为我们画出的这条拟合直线称为回归线。用公式表达为:
$$ (y _ {1实际} - y_{1预测})^2 + (y_{2实际}- y_{2预测})^2 + … + (y_{n实际} - y_{n预测})^2 $$
因为$y$的预测值可以由函数$ ax + b $求得,所以代入上面的公式可得:
$$ F(a,b) = \sum_{i=1}^n(y_i-(ax_i + b))^2 $$
所以监督学习中的线性回归方法就是通过大量的数据样本由机器求得$a$和$b$的值,使得函数$F$的值最小,那么回归线也就求出来了,既称为算法收敛。
如何求函数的最小值
说到函数的最小值,那就要引入导数这个数学工具了,下面我从几何角度来解释什么是导数,它和函数的最小值有什么关系。
导数与斜率
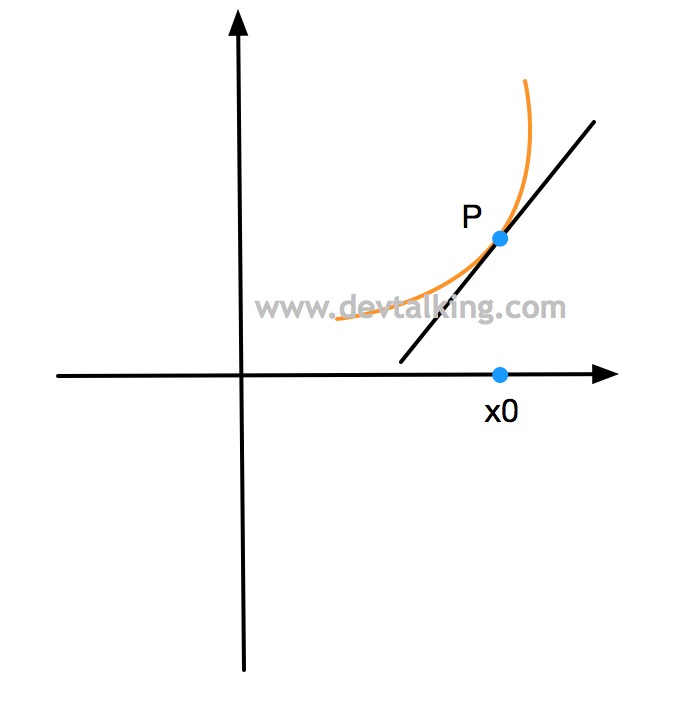
如上图所示,在图中的二维坐标系中,有一条曲线,一条直线,该直线为曲线的切线,相交于点$P$,该点的$x$轴坐标值为$x_0$。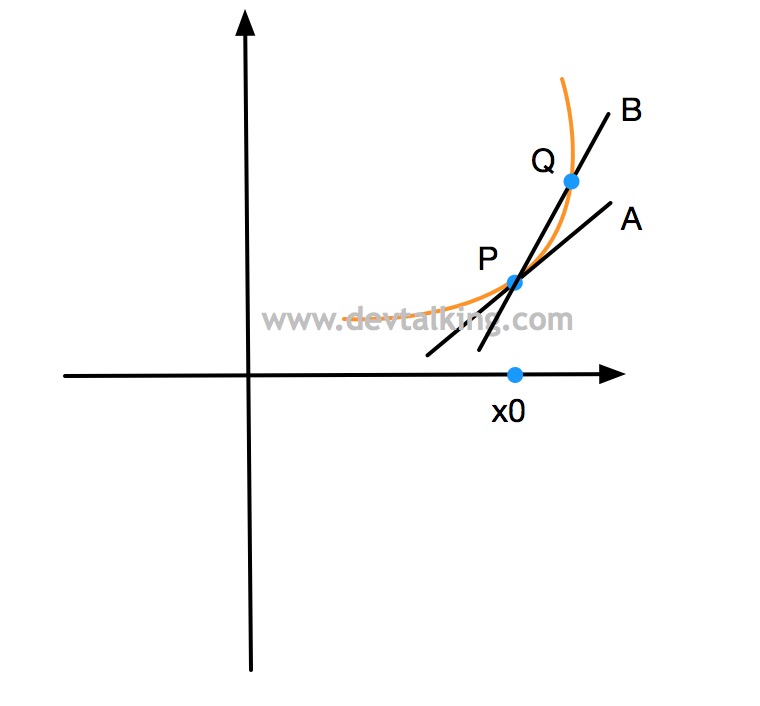
如上图所示,我们再画一条直线$B$,使其经过曲线上的点$P$和点$Q$,直线$B$称为曲线的割线。当点$Q$逐渐接近点$P$时,直线$B$就会逐渐接近直线$A$,所以说切线其实是割线的极值。
如上图所示,$\Delta x$表示$x$的变化量,并且我们假设直线$B$的函数为$f(x)$,那么$\Delta f$表示函数$f$的变化量。在几何学中,一条直线关于横坐标轴倾斜程度的量,称为斜率,并且定义对于两个已知点$(x_1,y_1)$和$(x_2,y_2)$,如果$x_1$不等于$x_2$,则经过这两点直线的斜率为$k=(y_1-y_2)/(x_1-x_2)$。
所以直线$B$的斜率为$k=\Delta f / \Delta x$。因为点$P$和$Q$的坐标分别为$(x_0,f(x_0))$和$(x_0+\Delta x,f(x_0+\Delta x))$,所以我们代入可得:
$$ k=\frac {f(x_0+\Delta x) - f(x_0)} {(x_0+\Delta x)-x_0}=\frac {f(x_0+\Delta x) - f(x_0)} {\Delta x}$$
上文中说到切线其实是割线的极值,那么切线$A$的斜率就是当$\Delta x$趋向于0时的值:
$$ k=\lim_{\Delta x->0}\frac {f(x_0+\Delta x) - f(x_0)} {\Delta x}$$
接下来我们再来看导数,导数是微积分中重要的基础概念,它描述了一个函数在某一点附近的变化率,如果函数的自变量和因变量都是实数的话,那么函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率:
$$ k=df=\lim_{\Delta x->0} \frac {f(x_0+\Delta x) - f(x_0)} {\Delta x} $$
极值
在数学中,极大值与极小值是指在一个域上函数取得最大值或最小值的点的函数值。这个域可以是整个函数域,也可以是整个函数域中的局部域。所以一个函数有局部极大极小值,也有全局极大极小值。
说到极值,又不得不说到微积分中的另外一个概念,驻点。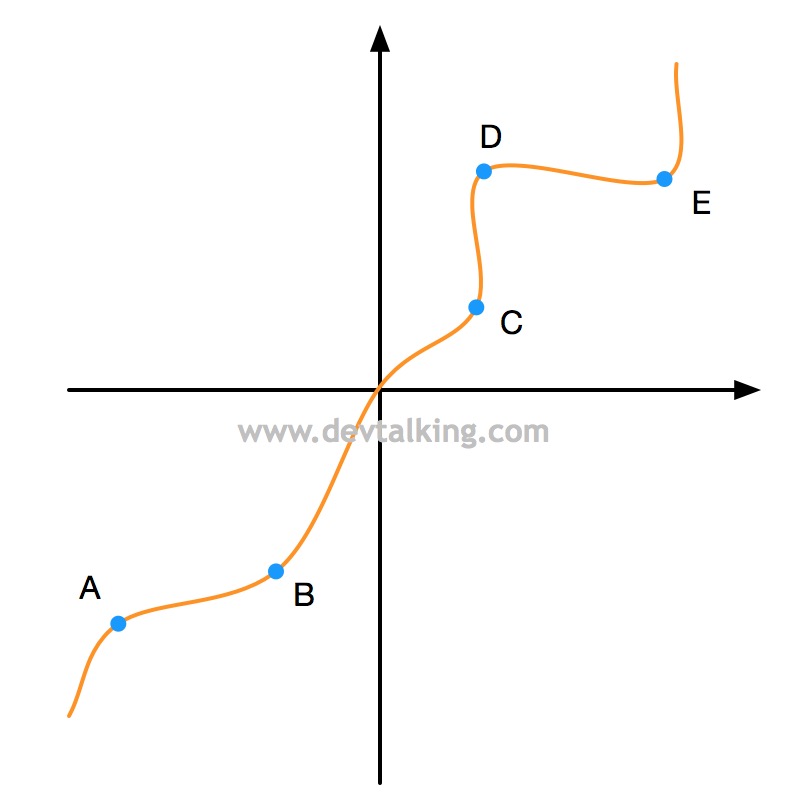
如上图所示,在二维坐标中展示了一个一元函数的曲线,点$A$、$B$、$C$、$D$、$E$都是该曲线上的局部极大值或局部极小值,这些点就称为驻点。在每个驻点,函数在该域的输出值停止增加或减少,即变化率为零。每个驻点其实就是局部域曲线的切点。结合上文中提到的导数是描述函数在某一点附近的变化率,所以可得一元函数的局部极值点的导数为零。
假设有一个一元函数$f(x)=x^2$,该函数的导数通过上面的导数公式可得$f’(x)=2x$,并且该函数代表的曲线为下凹曲线,所以该函数的最小值为$f’(x)=0$,即当$x$等于0时$f(x)$的值最小。
二元函数的最小值
上文中$F(a,b)$是一个二元函数,实质上道理一样,我们可以把二元函数图像设想成一个像碗一样的曲面,那么最小值就是碗底,即曲面的最凹陷部,那么从360度任意方向上看,偏导数都是0。
偏导数
在数学中,一个多元函数的偏导数是它关于其中一个变量的导数,而保持其他变量恒定。全导数自然就是所有变量的导数。函数$f$关于变量$x$的偏导数写为$f’_x$或$\frac {\partial f}{\partial x}$,偏导数符号$\partial$是全导数符号$d$的变体。
因为曲面上的每一个点都有无穷多条切线,所以描述这种函数的导数非常困难,所以通常选择其中一条切线,并求出它的斜率,将其他变量视为常量,这就是偏导数。
所以$ F(a,b) = \sum_{i=1}^n(y_i-(ax_i + b))^2 $的最小值就是分别求$a$和$b$的偏导数,然后可以得到一个关于$a$和$b$的二元方程组,就可以求出$a$和$b$了,这个方法被称为最小二乘法。
$F(a,b)$的最小值
首先我们把$F(a,b)$展开:
$$ F(a,b) = \sum_{i=1}^n(y_i-(ax_i + b))^2 \\
=(y_1-(ax_1 + b))^2+(y_2-(ax_2 + b))^2+…+(y_n-(ax_n + b))^2 \\
=(y_1^2-2y_1(ax_1+b)+(ax_1+b)^2)+(y_2^2-2y_2(ax_2+b)+(ax_2+b)^2) \\
+…+(y_n^2-2y_n(ax_n+b)+(ax_n+b)^2) \\
=y_1^2-2ay_1x_1-2by_1+a^2x_1^2+2abx_1+b^2+y_2^2-2ay_2x_2-2by_2+a^2x_2^2+2abx_2+b^2 \\
+…+y_n^2-2ay_nx_n-2by_n+a^2x_n^2+2abx_n+b^2 \\
=(y_1^2+..+y_n^2)-2a(x_1y_1+..+x_ny_n)-2b(y_1+..+y_n) \\
+a^2(x_1^2+..+x_n^2)+2ab(x_1+..+x_n)+nb^2 $$
然后利用平均数,把上面式子中每个括号里的内容进一步简化,比如:
$$\frac {(y_1^2+..+y_n^2)} n=\overline {y^2}$$
则:
$$(y_1^2+..+y_n^2)=n\overline{y^2}$$
所以$F(a,b)$可以继续简化为:
$$F(a,b)=n\overline{y^2}-2an\overline{xy}-2bn\overline y+a^2n\overline{x^2}+2abn\overline x+nb^2$$
然后我们分别对$a$和$b$求偏导数,并且令偏导等于0:
$$\frac {\partial F}{\partial a}=-2n\overline xy+2an\overline {x^2}+2bn\overline x=0$$
$$\frac {\partial F}{\partial b}=-2n\overline y+2an\overline x+2nb=0$$
消掉$2n$最后得到关于$a$,$b$的二元方程组为:
$$-\overline {xy}+a\overline {x^2}+b\overline x=0$$
$$-\overline y+a\overline x+b=0$$
最后得出a和b的求解公式:
$$a=\frac {\overline x \overline y-\overline {xy}} {(\overline x)^2-\overline {x^2}}$$
$$b=\overline y-a\overline x$$
将上文中的那组数据带入后可算的$a$和$b$的值:
从带入结果来看,这条回归线的函数为$f(x)=14.93x-360.88$,现在我们就可以通过回归线来做一些预测,比如上图中计算了面积为35.5平方米和55.26平方米房子的售价,分别为169.29万和464.4万。
评价回归线的拟合程度
因为我们画出的拟合直线只是一个近似值,所以需要有一个标准来评判回归线拟合程度的好坏,即算法收敛情况。我们来看几个概念:
总偏差平方和
总偏差平方和又称总平方和(SST,Sum of Squares for Total),是每个因变量的实际值与因变量的平均值的差的平方和,即反映了因变量取值的总体波动情况:
$$SST=\sum_{i=1}^n(y_i-\overline y)^2$$
回归平方和
回归平方和(SSR,Sum of Squares for Regression)是因变量的回归值(回归线上的$y$值)与其平均值的差的平方和。它是由于自变量$x$的变化引起的$y$的变化,反映了$y$的总偏差中由于$x$与$y$之间的线性关系引起的$y$的变化部分:
$$SSR=\sum_{i=1}^n(\hat y_i-\overline y)^2$$
误差平方和
误差平方和(SSE,Sum of Squares for Error)是因变量的各实际值与回归值的差的平方和,反映了除$x$对$y$的线性影响之外的其他因素对$y$变化的作用:
$$SSE=SST-SSR$$
因为总偏差是包含了所有可能对$y$值有影响的因素,比如房子的售价不可能只有面积来决定,还包括地域、户型、楼层、楼龄等等因素。回归平方和只包含$x$对$y$变化的影响,即只是面积对售价的影响。
所以拟合优度$R^2=SSR/SST$或者$R^2=1-SSE/SST$,$R^2$的取值范围在0到1之间,越接近1说明拟合程度越好,说明$x$对$y$值的影响权重越大。
比如如果所有的点都在回归线上,那说明$SSE$等于0,则$R^2=1$,说明$y$的变化100%由$x$的变化引起,没有其他因素会影响$y$,则回归线能够完全解释$y$的变化,如果$R^2$的值很低,则说明$x$和$y$之间可能根本就不存在线性关系。
将数据带入计算得出最拟合优度为0.92,拟合程度还不错,说明在特定的望京区域内房屋面积是主要影响价格的因素。
总结
我认为从线性回归开始学习机器学习是最好的切入点,而且线性回归也是监督学习最根本的支撑,比如梯度下降等算法都需要基于线性回归的知识来理解。另外在我看来人工智能(AI)并不是要造一个机器人脑,这是伪科学。人工智能只是利用机器强大的计算能力,用数学工具,通过对大量数据的统计分析从而得出近似最优答案。所以说,人类和AlphaGO下棋,不是输在智力,而是输在身体机能。